无干扰、传递性和通道控制安全策略
摘要
我们考虑到在“干扰”关系中安全策略的非干扰公式是非传递的。这些策略为一些实际的安全问题提供了形式化的基础,例如通道控制和可信路径。我们证明了对于非传递的情况,合适的无干扰模型是Haigh和Young为“多域安全”(MDS,multidomain security)开发的公式。我们构造了一种非传递策略的“单步展开定理”,并证明了它与Haigh和Young的展开定理有显著的不同。我们认为他们的定理是错误的。一份配套报告提出了一个机械检查的形式规范,并验证了我们的定理。
我们考虑传递和非传递之间的关系来模拟安全性。我们证明了无干扰和展开定理的标准公式与我们的非传递公式完全对应,专门用于传递情况。我们证明了传递策略正是“多级安全”(MLS,multilevel security)策略,并且任何MLS安全系统都满足展开定理的条件。
我们还考虑了安全性的无干扰公式和访问控制公式之间的关系,并确定了在建立访问控制实现的可靠性方面起关键作用的“参考监视器假设”。
Chapter 1 Introduction
Goguen和Meseguer引入了无干扰的概念,以便为安全策略及其执行机制的规范和分析提供形式化基础。除了费尔塔格(Feiertag)、莱维特(Levitt)和鲁宾逊(Robinson)的工作可以看作是戈格恩(Goguen)和梅斯格尔(Meseguer)之前工作的先驱,贝尔(Bell)和拉帕杜拉(La Padula)的工作最具影响力外,他们还制定了访问控制方面的安全措施。访问控制的构建存在许多困难。首先,因为它们是根据强制执行安全的机制来描述的,所以在这些机制证明不充分的情况下,它们没有提供指导。第二,很容易对访问控制策略进行不正当的解释,使其符合字面意思,但不符合策略的意图,以至于明显不安全。访问控制公式的支持者反驳说,解释或实现必须是模型的“真实表示”,但他们没有提供该术语的形式化定义。
相比之下,无干扰公式是纯粹的策略描述,虽然已经开发了一些技术来证明特定机制强制执行给定的无干扰策略,但没有承诺实施它们的特定机制。其次,无干扰策略具有逻辑理论的形式;任何作为理论模型的实现(即验证其公理)都是安全的。
无干扰的思想非常简单:如果安全域u执行的任何操作都不会影响v看到的后续输出,则安全域u与域v互不干扰。无干扰在为军事多级安全策略和验证其实现的方法提供形式化基础方面非常成功。
然而,有许多实际的安全问题似乎超出了不干涉公式的范围。其中之一是“通道控制”,首先由Rushby制定。信道控制安全策略可以用有向图表示,其中节点表示安全域,边表示允许的直接信息流。信道控制问题的范例是端到端加密控制器,如图1.1所示。
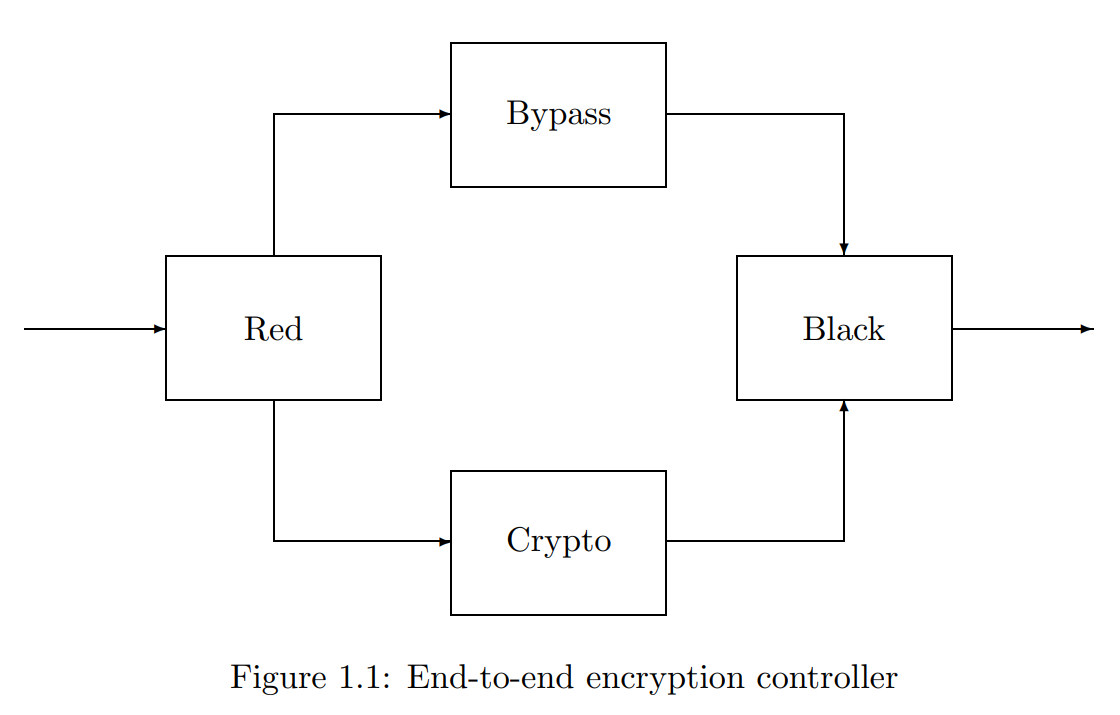
明文消息到达控制器的Red侧;它们通过加密设备发送;它们的报头必须保持为纯文本,以便网络交换机能够解释它们,通过旁路发送。邮件头和加密正文在Black部分重新组装,并发送到网络上。我们想在这里指定的安全策略是,信息从红色流向黑色的唯一通道必须是通过加密和旁路的通道。因此,许多信道控制策略的一个重要特征是,表示允许的信息流的边缘是不可传递的:允许信息通过加密和旁路从红色流到黑色,但不能直接这样做。
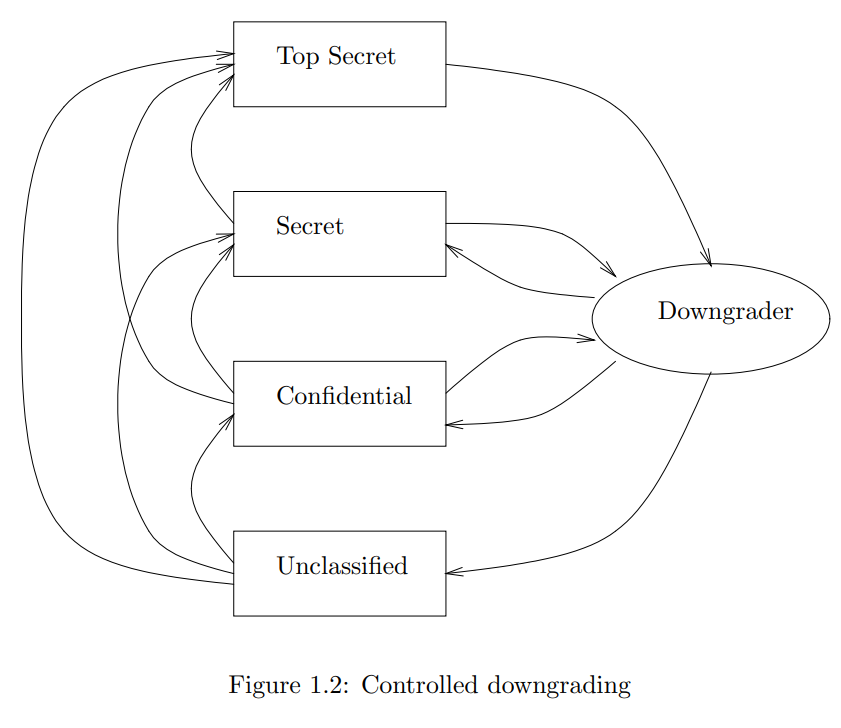
另一个示例如图1.2所示,其中传递元素和不传递元素相结合。左边的边表示美国使用的分类级别之间的传统传递流关系。右侧是进出特殊降级器域的边,这些边是非传递的。这些边表示的流是非传递的,因为尽管信息可以通过降级器从绝密域流向机密域,但它不能直接从绝密域流向机密域。因此,信息可以在安全级别上“向上”流动而不受限制,但只能通过可能受信任的降级器域的中介“向下”流动。
像刚才描述的那样的通道控制策略似乎能够指定一些超出标准安全建模技术范围的安全问题。Boebert和Kain有说服力地认为,一种称为“类型强制”的信道控制变体可以用来解决许多令人烦恼的安全问题。因此,一个有价值的挑战是为信道控制策略及其类似策略找到充分的形式化基础。
早期尝试提供一种形式化的方法来验证(虽然没有具体说明)信道控制策略是基于一种验证完全分离的技术。其想法是移除提供预期通道的机制,然后证明最终系统的组件是隔离的。这种方法最近被证明存在细微的缺陷,尽管建立完全分离的方法经过了相当严格的审查,只进行了少量的修改。
无干扰公式在解释多级安全策略方面的成功自然需要考虑信道控制的无干扰基础。然而,这是一个相当大的挑战。例如,很明显,图1.1的加密控制器的红色侧必然干扰黑色;我们需要找到一种说法,即这种干扰只能通过加密或旁路的中介发生。Goguen和Meseguer在其关于无干扰的原始论文中提出了一种方法,但该方法不正确。Goguen和Meseguer在他们关于这个主题的第二篇论文中认识到了这一点,他们对无干扰的基本公式进行了一些扩展。 然而,Haigh和Young对非传递行性无干扰策略给出了第一个真正令人满意的处理方法,第二年的版本更加完善。他们表明,有必要考虑在给定操作之后执行的操作的完整序列,以确定是否允许该操作干扰另一个域。例如,只有当加密或旁路有一些干预操作时,才允许红色域的操作干扰黑色域。
本报告这一部分的主要目的在说明信道控制安全策略可以由无干扰策略建模,其中“干扰”关系是非传递的,其中“干扰”的定义是Haigh和Young的定义。我们还表明,传统的多级策略是信道控制策略的特例,对应于那些“干扰”关系是传递的策略。我们表明,在这种特殊情况下,我们的结果与熟悉的结果不谋而合,从而为其准确性提供了一些额外的证据。
安全不干涉公式的一个重要组成部分是“展开”定理,该定理建立了足以确保系统安全的单个动作行为的条件。这些展开定理为形式化验证实现是否满足无干扰安全策略提供了实用方法的基础。本报告部分的主要结果是推导了信道控制情况下的展开定理。我们证明了这个定理与Haigh和Young的定理有显著的不同,并且我们认为他们的结果是不正确的。
信道控制情况下的无干扰和解绕的发展令人惊讶地复杂,鉴于之前失败尝试的历史,我们以相当正式的形式介绍了我们的发展,并详细描述了证明。本报告的附录第三部分描述了使用Ehdm形式规范和验证系统对我们的主要定理进行的形式化验证。
本报告的组成部分如下。在下一章中,我们将介绍安全标准无干扰公式的发展,然后考虑无干扰安全策略和访问控制策略之间的关系。这一发展旨在提供一个模型和基础,以便与后面给出的概括进行比较。第3章研究了非传递无干扰策略的情况,并认为这些策略在无干扰的标准表述中没有有用的解释。第3章的第2部分研究了传递策略的特殊性质,并表明它们与经典的多级安全是相同的。第4章提出了一种改进的无干扰公式,它确实为非传递性政策提供了一种有意义的解释,并推导了该解释的展开定理。第五章比较了传递式和不传递式的无干扰公式,并将我们的解卷定理与Haigh和Young的解卷定理进行了比较。第6章给出了我们的结论。附录给出了我们的非传递解卷定理的正式规范和验证,该定理已使用Ehdm验证系统进行了机械检查。
Chapter 2 Basic Noninterference
2.1 访问控制解释
在本章中,我们介绍了Goguen和Meseguer在无干扰断言方面的安全性公式的核心,以及相关验证技术的展开定理。我们的符号与Goguen和Meseguer的符号有很大不同,更类似于后来的作者,如Haigh和Young。
我们用传统的有限状态自动机对计算机系统进行建模。
定义1:系统$M$包含如下元素。
- $S$为系统状态集合,其中$s_0 \in S$表示系统初始状态。
- $A$表示动作集合。
- $O$表示输出集合。
一些函数包括$step$和$output$: - $step: S \times A \rightarrow S$
- $output: S \times A \rightarrow O$
我们通常使用s、t表示状态,a、b表示动作,$\alpha、\beta$表示动作序列。
动作可以被认为是机器要执行的“输入”、“命令”或“指令”; $step(s,a)$表示在状态$s$时发生动作$a$后的下一个状态。$output(s,a)$则表示该动作返回的结果。
- $run: S \times A^* \rightarrow S$
通过以下方程完成对动作序列的自然扩展
其中$\Lambda$表示空序列,$\circ$表示串联。
为了讨论安全性,我们必须假设一些安全“域”和限制这些域之间允许的信息流的策略。特定安全域的代理或主体通过向系统呈现动作并观察所获得的结果来与系统交互。因此,我们假设
- $D$表示安全域
- $dom: A \rightarrow D$表示安全域与动作的关联
我们使用u、v、w来表示域。
$\rightsquigarrow$表示有干扰。
我们希望从信息流的角度定义安全性,因此下一步是形式化地捕获“信息流”的概念。关键的观察结果是,当域u提交的操作导致域v感知到的系统行为与不存在这些操作时感知到的系统行为不同时,可以说信息正是从域u流向域v的。因此,我们定义了一个函数,该函数从操作序列中删除或“清除”所有由域提交的操作,这些操作需要不干扰给定域。如果给定域v无法区分机器在处理给定操作序列后的状态,以及在处理相同序列后清除需要与v互不干扰的操作后的状态,则机器是安全的。
定义2:对于$v\in D$和动作序列$\alpha \in A^*$,,我们将$purge(\alpha, v)$定义为$\alpha$的子序列,该序列通过删除与u相关的所有动作而形成,使得u与v无干扰。
我们通过以下确定安全性:
- $do:A^*\rightarrow S$
- $test:A^*\times A\rightarrow O$
当
且
时,若有
则认为系统是安全的。
机器在初始状态$s_0$下启动,并执行动作集合中的一个序列$\alpha\in A^*$,这导致机器产生一些列输出,并通过一系列状态前进,最终到达$do(\alpha)$。此时执行动作$a$并观察对应的输出$test(\alpha,a)$
安全的无干扰定义用动作序列和状态转换表示;为了获得验证系统安全性的简单技术,我们想推导出各个状态转换的条件。开发的第一步是将系统的状态划分为与给定域“看起来完全相同”的等价类。然后,验证技术将证明每个域的系统视图不受要求不干扰它的域的操作的影响。
定义3:对于每个域$u\in D$,存在等价关系
表示两个状态$s$和$t$在响应$u$的动作时产生的输出是相同的。
安全性的定义要求一个域看到的输出不受要求无干扰第一个域的其他域的操作的影响。下一个结果表明,对于输出一致的系统,如果“视图”同样不受影响,则可以实现安全性。
引理1:$\rightsquigarrow$表示策略,$M$表示满足视图隔离和输出一致性的系统。以便有
那么对于$\rightsquigarrow$,$M$是安全的。
证明:设引理中的$u=dom(a)$,有
输出一致性有
根据定义2,有
接下来,我们定义各个状态转换的约束。
定义4:$M$为视图隔离系统,$\rightsquigarrow$为策略。
原文
Rushby J. Noninterference, Transitivity, and Channel-Control Security Policies[M]. CSL-92-02, Menlo Park: Stanford Research Institute, 1992.