剑指Offer打卡

发表于 | 更新于: | 分类于 | 本文总阅读量 次
字数统计: 3.1k | 阅读时长 ≈ 14

剑指Offer第二版
https://www.acwing.com/problem/search/1/?csrfmiddlewaretoken=Y5IpedXu3Sl5DfZekji1hxNwdx39jFGAZnymRUdbGvocdSTYVoacOQ44UmneUfw4&search_content=%E5%89%91%E6%8C%87

Group1

数组中重复的数字

https://www.acwing.com/problem/content/14/

  1. 先遍历数组，若有超过区间 [0, n-1] 的数值，就直接返回 -1
  2. 再遍历一次数组，如果当前位置的数值与下标不一样。
    • 且数值对应的那个下标与当前位置的值不同，就交换它们的位置。
    • 若一样，则说明找到了重复元素了
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
public:
    int findRepeatNumber(vector<int>& nums) {
        int n = nums.size();
        for (int x : nums) 
            if (x < 0 || x >= n)
                return -1;
        for (int i = 0; i < n; ++i) {
            if (i != nums[i]) {
                if (nums[i] != nums[nums[i]]) swap(nums[i], nums[nums[i]]);
                else return nums[i];
            }
        }
        return -1;
    }
};

不修改数组找出重复的数字

https://www.acwing.com/problem/content/15/

  • 抽屉原理：将 n+1 个苹果放进 n 个抽屉，必然会有两个苹果在一个抽屉的情况

分治（二分）的思想，根据数值大小（注意不是下标）将整个区间一分为二。

  • 因为数值范围是 [1, n]，所以假设总共有 n 个坑位。也就是说
  • 又因为共有 n+1 个数，所以，起码会有一边数的个数会大于坑位的个数。
  • 不断找到这个区间并再次划分左右，直到区间内只存在一个数，这个数就一定是重复数字
1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    int duplicateInArray(vector<int>& nums) {
        int l = 1, r = nums.size() - 1;
        while (l < r) {
            int mid = l + ((r-l) >> 1);
            int s = 0;
            for (int i : nums) s += i >= l && i <= mid;  // 这里的s用来累计需要放在左区间中的数值个数的，如果nums中某数在[l,mid]就确定在左区间，s就加1
            if (s > mid - l + 1) r = mid;  // 左区间内数值个数大于左区间坑位则将右边界左移到mid
            else l = mid + 1;  // 说明右区间数值个数大于坑位，左边界右移到mid+1
        }
        return r;
    }
};

二维数组中的查找

https://www.acwing.com/problem/content/16/

这里可以看出，第 0 行的最后一列是该行最大，该列最小。所以从矩阵的右上角开始遍历。

  • 正好等于目标值直接返回 true
  • 大于目标值，说明目标一定在更小的列
  • 小于目标值，则一定在更大的行

image-20210705225035681

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    bool findNumberIn2DArray(vector<vector<int>>& matrix, int target) {
        if (matrix.size() == 0 || matrix[0].size() == 0) return false;  // 检查边界
        int i = 0, j = matrix[0].size() - 1;
        while (i < matrix.size() && j >= 0) {
            if (matrix[i][j] == target) return true;
            else if (matrix[i][j] > target) --j;
            else ++i; 
        }
        return false;
    }
};

替换空格

https://www.acwing.com/problem/content/17/

https://leetcode-cn.com/problems/ti-huan-kong-ge-lcof

  • 很简单，开一个新字符串，再遍历源字符串，遇到空格就加 %20，否则就加原字符
1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    string replaceSpace(string s) {
        string ans = "";
        for (auto i : s) {
            if (i == ' ') 
                ans += "%20";
            else
                ans += i;
        }
        return ans;
    }
};

从尾到头打印链表

https://www.acwing.com/problem/content/18/

https://leetcode-cn.com/problems/cong-wei-dao-tou-da-yin-lian-biao-lcof/

  • 创建数组，遍历链表，依次将值压入数组
  • 逆序返回
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    vector<int> reversePrint(ListNode* head) {
        vector<int> res;
        while (head) {
            res.push_back(head->val);
            head = head->next;
        }
        return vector<int>(res.rbegin(), res.rend());
    }
};

重建二叉树

https://www.acwing.com/problem/content/23/

https://leetcode-cn.com/problems/zhong-jian-er-cha-shu-lcof/

  • 先用哈希表记录中序遍历每个值的位置，以便于后面找根节点位置
  • 搜索过程中
    • 先判断序列长度，如果序列为空就返回空指针
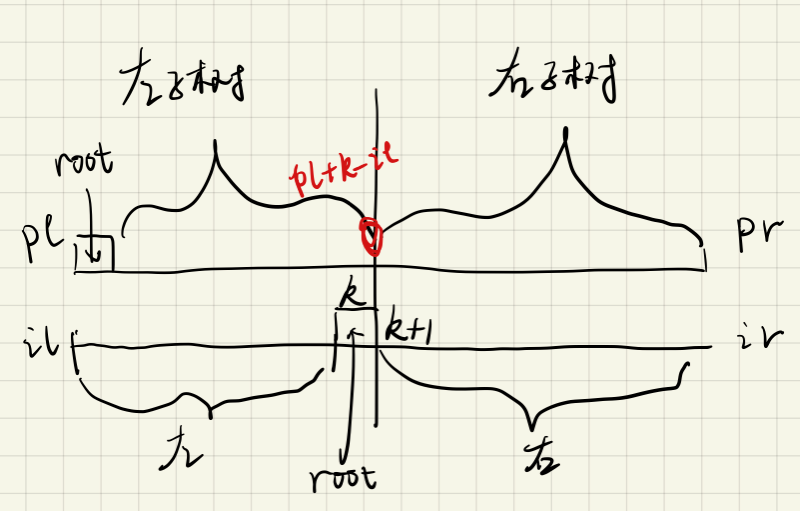
    • 然后前序遍历的左边界值 preorder[pl] 一定是根节点，根据这个值在哈希表中找到中序遍历的位置
    • 分别递归求出下一个左子树及右子树，然后插到 root 上就可以恢复二叉树了

其中 dfs 的几个参数前两个分别为前序遍历的左右边界，后两个分别是中序遍历的左右边界。求下一个左右子树时，区间范围的确定可以参考下图

image-20210706212029101

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    map<int,int> hash;
    vector<int> preorder, inorder;
    TreeNode* buildTree(vector<int>& _preorder, vector<int>& _inorder) {
        preorder = _preorder;
        inorder = _inorder;
        // 用 hash 表记录根节点在中序数组中的位置
        for (int i = 0; i < inorder.size(); ++i) {
            hash[inorder[i]] = i;
        }
        return dfs(0, preorder.size()-1, 0, inorder.size()-1);
    }

    TreeNode* dfs(int pl, int pr, int il, int ir) {
        if (pl > pr) return nullptr;
        auto root = new TreeNode(preorder[pl]);  // 根节点就是前序遍历的第一个节点
        int k = hash[root->val]; // 在中序遍历的位置为 k
        auto left = dfs(pl+1, pl+k-il,il,k-1);  // 左子树区间
        auto right = dfs(pl+k-il+1, pr, k+1, ir); // 右子树区间
        root->left = left, root->right = right;
        return root;
    }
};

二叉树的下一个节点

https://www.acwing.com/problem/content/31/

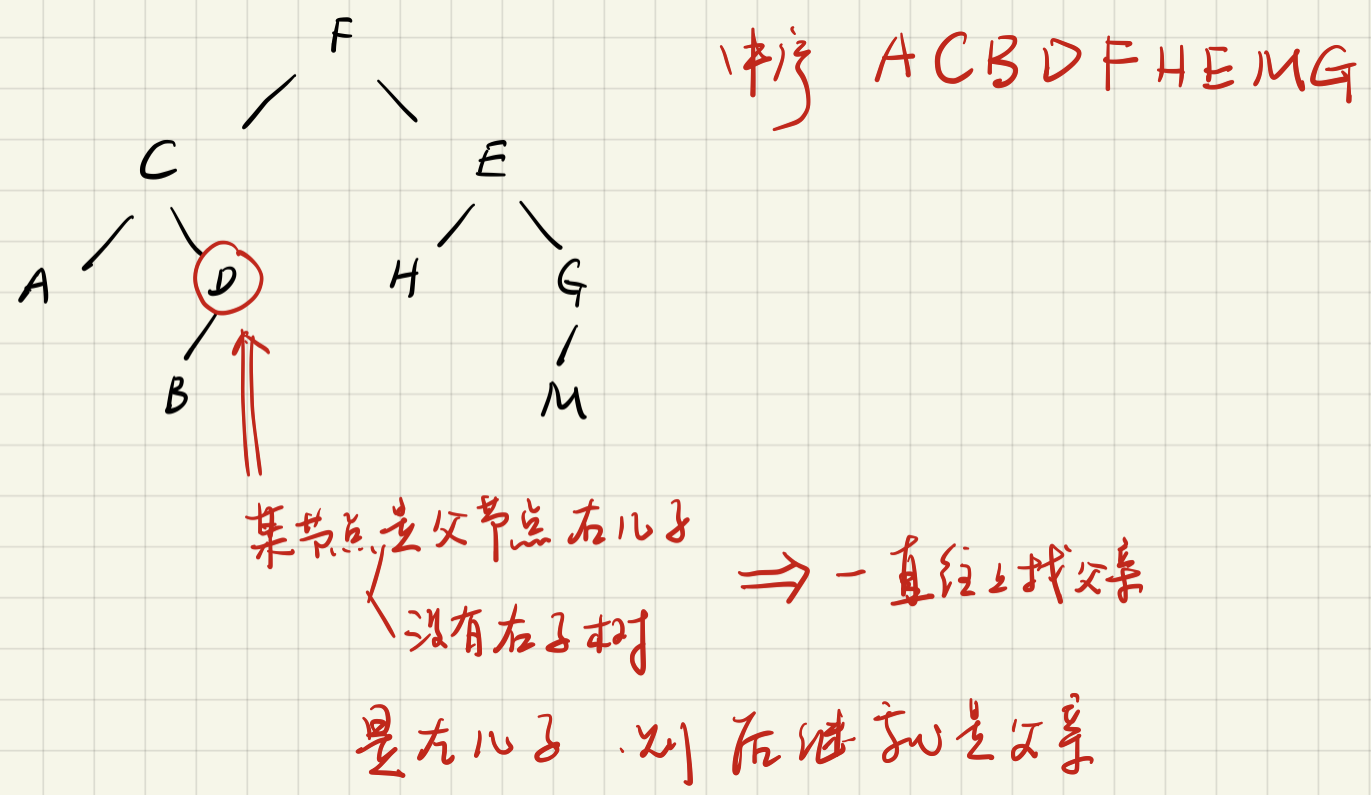
  • 情况一：如果某节点有右子树，那么右子树的最左侧节点就是后继
  • 情况二：没有右子树。
    • 该节点是其父亲的右儿子：一直往上找父亲，直到父亲为 NULL
    • 该节点是父亲的左儿子：其父亲就是后继（因为中序）

4ff4e3a3a28869c6

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode *father;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL), father(NULL) {}
 * };
 */
class Solution {
public:
    TreeNode* inorderSuccessor(TreeNode* p) {
        if (p->right) {
            p = p->right;
            while (p->left) p = p->left;
            return p;
        }
        
        while (p->father && p == p->father->right) p=p->father;
        return p->father;
    }
};

Group2

机器人的运动范围

https://www.acwing.com/problem/content/22/

https://leetcode-cn.com/problems/ji-qi-ren-de-yun-dong-fan-wei-lcof/

  • BFS
    • 将 {0,0} 压入队列，如果坐标各位之和满足要求，且没有被遍历过则结果 res 加 1
    • 后面的 for 循环用于对坐标的移动，因为从最左上角开始，所以横纵坐标只需要朝着右下移动即可。所以 dx 和 dy 只需要两个维度，遍历到的坐标都压入队列中。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
class Solution {
public:
    // 计算一个数字的各位之和
    int get_single_sum(int x) {
        int s = 0;
        while(x) s += x%10, x/=10;
        return s;
    }

    // 计算坐标数位之和
    int get_sum(pair<int,int> p) {
        return get_single_sum(p.first) + get_single_sum(p.second);
    }
    
    // 注意参数顺序，acwing 和 leetcode 参数顺序不同
    int movingCount(int threshold, int rows, int cols)
    {
        int res = 0;
        if (!rows || !cols) return 0; // 行列为0就返回0
        vector<vector<bool>> st(rows, vector<bool>(cols));  // 判断某个格子是否已经走过
        queue<pair<int,int>> q; // 记录坐标
        q.push({0,0}); 
        while (q.size()) {
            auto t = q.front();
            q.pop();
            // 如果大于阈值或者已经走过，就 continue
            if (get_sum(t) > threshold || st[t.first][t.second]) continue;
            res++;
            st[t.first][t.second] = true; // 标记一下，走过了

            // 因为从 0,0 开始，所以需要扩展移动，可能向上下左右移动
            // 可以定义两个一维数组，表示向量，以对应横纵坐标，dx和dy分别表示横纵坐标
            // {右,下}
            int  dx[2] = {0,1} , dy[2] = {1,0};
            for (int i = 0; i < 2; i++) {
                int x = t.first + dx[i], y = t.second + dy[i];
                if (x >= 0 && x < rows && y >= 0 && y < cols) {
                    q.push({x,y});
                }
            }
        }
        return res;
    }
};

剪绳子

https://www.acwing.com/problem/content/24/

https://leetcode-cn.com/problems/jian-sheng-zi-lcof/

我们假设 $N>0$，可以将 $N$ 分隔成若干份，有 $N=n_1+n_2+n_3+…+n_k$

  1. 假设存在其中一个数值 $n_i>=5$，但是如果我们从这个数值中分出一个 3 来，再构造乘积，其结果一定是大于等于 $n_i$ 的，也即有 $3\times(n_i-3)\geq n_i$。证明如下：

    由上式可得 $3\times n_i-9\geq n_i$

    则 $n_i\geq 4.5$ 这是满足假设条件的，所以 $3\times(n_i-3)\geq n_i$ 一定成立，因此分割后的值一定不会存在大于等于 5 的情况

  2. 假设存在一个数值等于 4，而 4 可以分为 $2\times2$，没有影响，所以也可以不存在 4

  3. 假设存在三个 2，也即 $2\times2\times2$，但是这个被分割的值原本为 6，可以分成 $3\times3$ 显然比分成三个 2 要大。

所以，综上，数值最终由 2 和 3 组成，2 的个数不超过 3 个。如果 2 的个数为 2，实际上就对应假设二，这个时候将结果乘以 4 并将值减去 4，就排除了这种情况，剩下只有一个 2 和若干 3 的情况。

1
2
3
4
5
6
7
8
9
10
11
class Solution {
public:
    int cuttingRope(int n) {
        if (n <= 3) return n-1;
        int res = 1;
        if (n % 3 == 1) res *= 4, n-=4;  // 两个 2 的情况
        if (n % 3 == 2) res *= 2, n-=2;  // 一个 2 的情况
        while (n) res *= 3, n-=3;
        return res;
    }
};

二进制中 1 的个数

https://www.acwing.com/problem/content/25/

https://leetcode-cn.com/problems/er-jin-zhi-zhong-1de-ge-shu-lcof/

这里需要对无符号数进行移位，否则，右移会补符号位。

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    int NumberOf1(int _n) {
        unsigned int n = _n;
        int ans = 0;
        while (n > 0) {
            if (n & 1) ans += 1;
            n >>= 1;
        }
        return ans;
    }
};

数值的整数次方

https://www.acwing.com/problem/content/26/

https://leetcode-cn.com/problems/shu-zhi-de-zheng-shu-ci-fang-lcof/

常规做法（超时）

1
2
3
4
5
6
7
8
9
class Solution {
public:
    double Power(double x, int n) {
        double res = 1;
        for (int i = 0; i < abs(n); ++i) res *= x;
        if (n < 0) res = 1/res;
        return res;
    }
};

快速幂 参考

思想是二分。推导过程如下：

  • $x^{n}=x^{\frac{n}{2}}\times x^{\frac{n}{2}}=(x^2)^{\frac{n}{2}}$

    • 当 $n$ 为偶数：$x^n=(x^2)^{n//2}$ (//为整除)
    • 当 $n$ 为奇数：$x^n=x\times (x^2)^{n//2}$ 会多出一个 $x$

  • 循环执行 $x=x^2$ 的赋值操作，将幂从 $n$ 将为 $\frac{n}{2}$ 直至 0

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    double myPow(double x, int _n) {
        if (x == 0) return 0;
        double res = 1;
        long n = _n;  // 防止n取到负数边界，导致转正数时溢出
        if (n < 0) x = 1/x, n = -n;  // 将n<0的问题转为n>0
        while (n) {
            if (n & 1) res *= x;  // n为奇数时需要多乘一个x
            x *= x;  // n除以2，将x^2给到x，逐渐降低幂次
            n >>= 1;
        }
        return res;
    }
};

删除链表结点

https://leetcode-cn.com/problems/shan-chu-lian-biao-de-jie-dian-lcof/

如果下一节点不为空，当下一节点值满足期望时，将下一节点的下一节点的指针给到当前节点的下一节点即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode* deleteNode(ListNode* head, int val) {
        ListNode* _dummyHead = new ListNode(0);  // _dummyHead就不需要判断head是不是头结点
        _dummyHead->next = head;
        ListNode* cur = _dummyHead;
        while (cur->next != NULL) {
            if (cur->next->val == val) {
                cur->next = cur->next->next;
                break;
            }
            cur = cur->next;
        }

        return _dummyHead->next;
    }
};

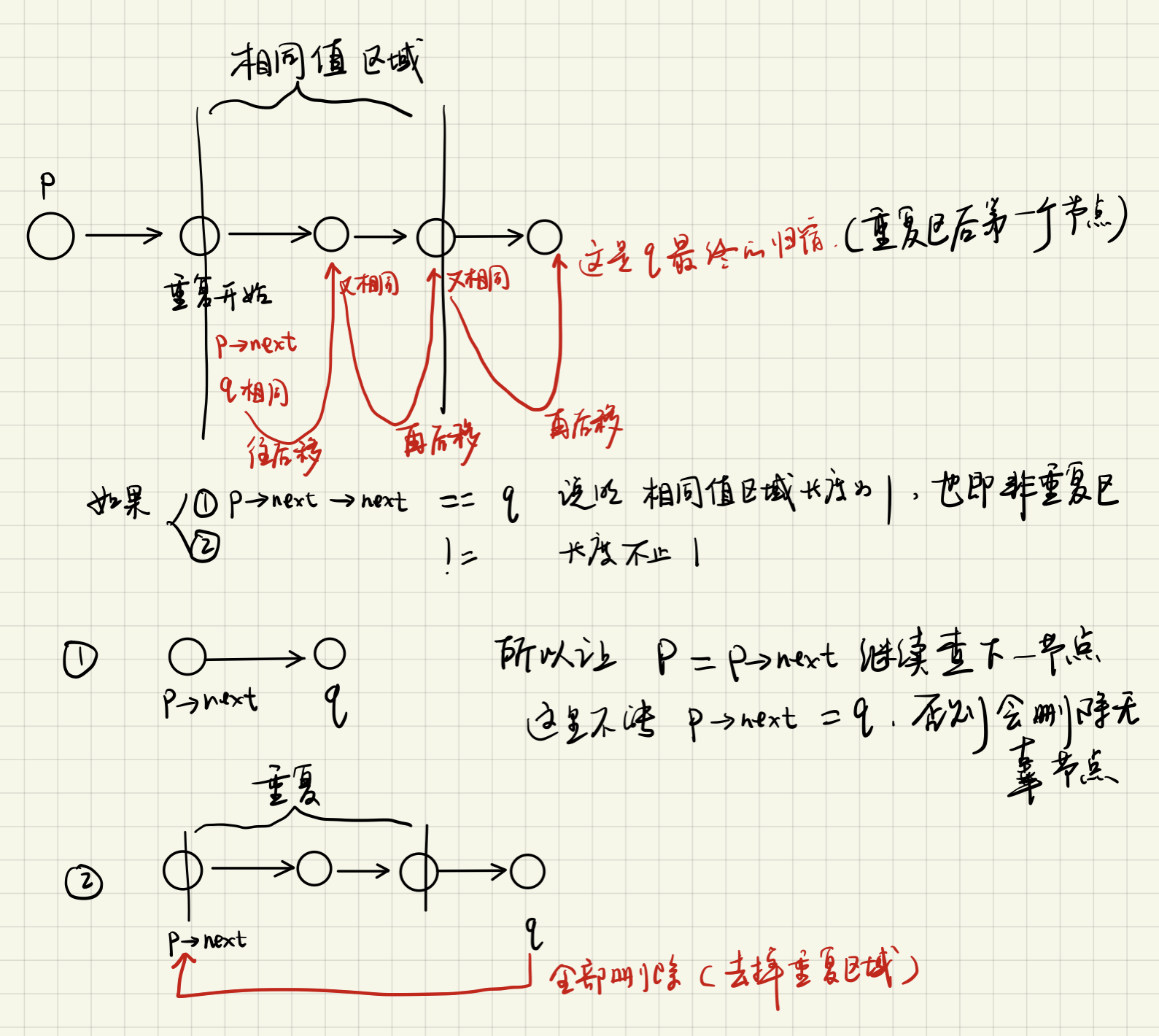
删除链表中重复的节点

https://www.acwing.com/problem/content/27/

-56e05a265f03026c

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode* deleteDuplication(ListNode* head) {
        // 虚拟头节点可以简化代码，否则如果删除头结点会比较麻烦
        ListNode* dummy = new ListNode(0);
        dummy->next = head;
        ListNode* p = dummy;
        while (p->next) {
            auto q = p->next;  // 为了知道重复节点的区域长度（实际上是开了一个新结构，然后比对值），
            while (q && p->next->val == q->val) q = q->next;
            if (p->next->next == q) p = p->next; 
            
            else p->next = q;    
        }
        return dummy->next;
    }
};

正则表达式匹配

https://www.acwing.com/problem/content/28/

f[i][j]表示p从j开始到结尾，是否能匹配s从i开始到结尾

  1. p[j]是正常字符，f[i][j]=s[i]==p[j]&&f[i+1][j+1]
  2. p[j]是”.”，f[i][j]=f[i+1][j+1]
  3. p[j+1]是”“，s[i]==p[j]&&f[i][j]=f[i+1][j]||f[i][j+2]（类似 `b`这种情况）


----------- 本文结束 -----------




0%