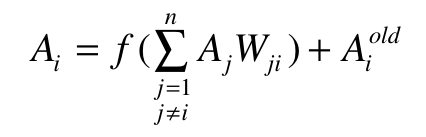模糊认知图(Fuzzy Cognitive Map,FCM)基本结构与原理
结构
- 基本的关系:
模糊认知图(FCM) = 模糊逻辑(Fuzzy logic) + 神经网络(Neural Network)
- 组成结构[1]
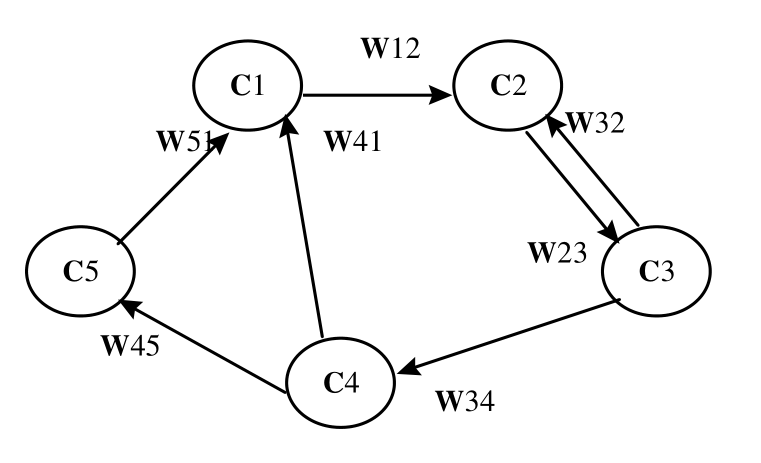
模糊认知图是有向图,它由表示概念(concept)的节点和带有权值(weight)的弧线组成。模糊认知图中的所有值都是模糊值,比如可以取值:concept value ∈ [0,1] weight value ∈ [-1,1]。一个concept可以影响其他的concept,同时,可以在构造模糊认知图的过程中不断增减互连关系或concept。一个具有n个概念节点的模糊认知图,可以用一个nxn阶矩阵W唯一确定。
原理
每个concept都代表着系统的一项特征,它们可能用于表征系统中事件、行为、目标等。每个concept的值用一个数字Ai表示,这个值由系统变量的真实值转换而成。
两个concept:Ci与Cj之间的关系分三种情况:
Wij > 0 Ci与Cj正相关
Wij < 0 Ci与Cj负相关
Wij = 0 Ci与Cj无因果关系
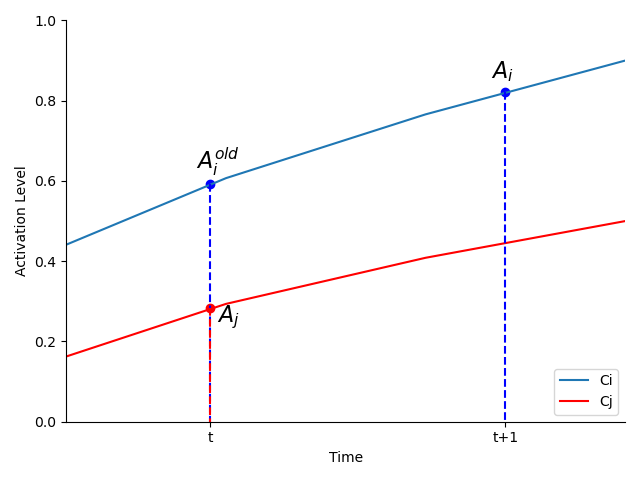
影响当前concept值(Ai)的因素有:该concept前时刻的值Aiold + 所有与它相连的其它concept值乘以权值后的总和。
基本的应用方法
首先由若干专家确定最适合描述该系统的concept(可以是系统的特征、状态、变量、系统的输入或输出等),并给定一个模糊值(fuzzy value)来表征concept之间的互连关系(正/负相关)
以上提到的模糊值(权值)需要考虑:
a. 权重的符号,Ci是否会影响Cj
b. Ci对Cj的影响程度
反之亦然。
然后整合这些专家的意见,此时需要给每位专家一个信誉值(credibility),在整合前,给每位专家的FCM乘以他们对应的信誉值。
经过初始化后的FCM,其中的concept根据设定会相互影响,直到:
a. 到达平衡 或
b. 到达限定周期 或
c. 出现混沌行为
以上的结果是:构造单个FCM
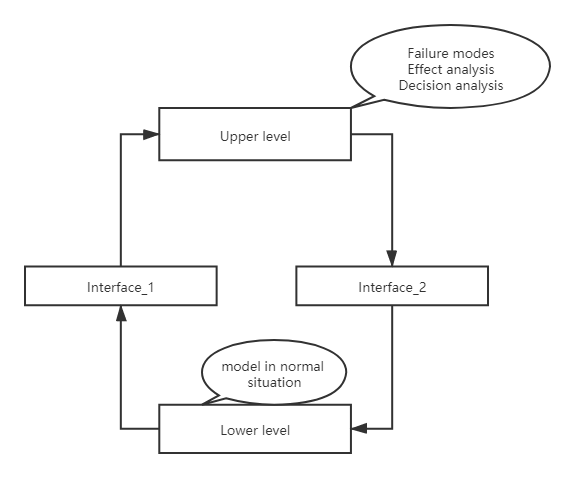
但有时,我们还需构造多个FCM去描述系统的不同模块,然后用类似的方法将它们集成到一个增强的FCM中。
tip: 当构造多个不同模块的FCM(如两层FCM)后,其中某个FCM中的部分concept可能会影响其他FCM的concept。
训练方法
目的:调整权值weight
可能的方法:
a. Differential Hebbian learning (DHL,微分Hebbian学习方法)是一种无监督的学习方法,未在实际系统中广泛运用[2]。
b. Nonlinear Hebbian learning (NHL,非线性Hebbian学习方法)[3]
非线性 Hebbian 算法是一种无监督权值学习方法,在系统权值学习具有广泛的应用。它利用权值关联的原因节点状态值与结果节点状态值的乘积对连接权值进行无向修正 , 没有其他约束条件来提高学习效率和模型准确度。
四种非监督学习方法[4]
1. Signal Hebbian
- 关联局部神经元信号。
- 如果神经元i和神经元j同步激活,则突触能量增强或突触能量减弱。
2. Competitive
- 用0-1竞争信号(神经元j的信号)调制信号突触差异。
- 突触只在突触后神经元获胜时才学习。
- 突触后神经元编码突触前信号模式。
3. Differential Hebbian
- 关联信号速度和神经元信号。
- 通过神经元信号的微分获得信号速度。
4. Differential Competitive
- 结合Competitive和Differential Hebbian
- 仅在有变化时学习
神经网络的基本结构与原理
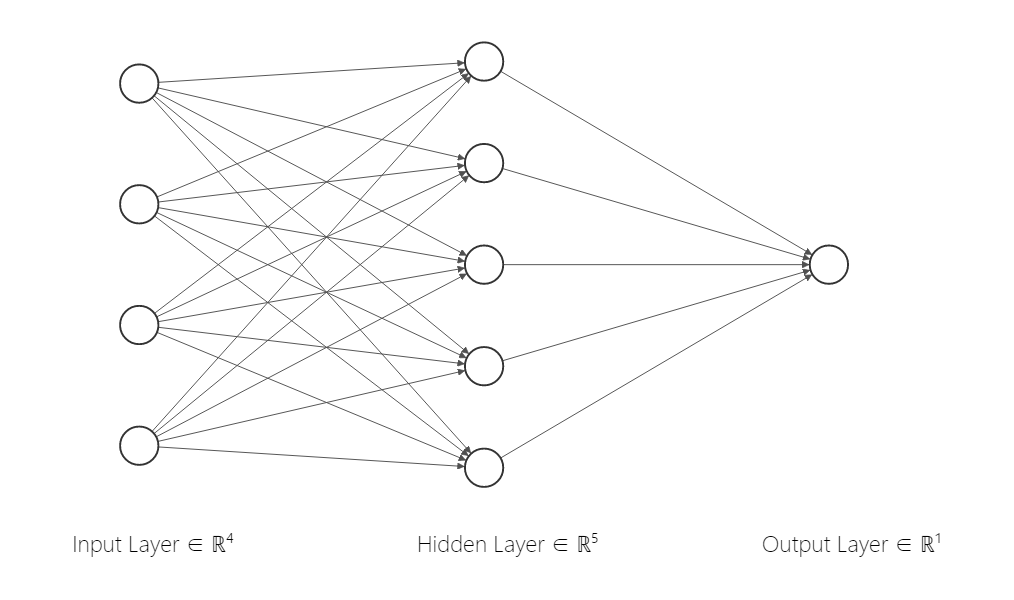
结构
原理[5]
随机生成神经元间的权值
对输入层神经元的数据加权求和再用激励函数激活,得到隐藏层的值
用类似的方法加权求和并激活,得到输出层的值
计算以上得到的输出层的值,与训练集中数据相比的误差大小(误差趋近于0收敛)
根据误差大小,计算残差
输出层残差值加权求和,得到隐藏层的残差
隐藏层残差加权求和。。。
根据残差值调整权值
如何进行训练
如以上,梯度下降法
Reference
[1] Stylios C , Georgopoulos V C , Groumpos P P . The Use of Fuzzy Cognitive Maps in Modeling Systems[C]// 5th IEEE Mediterranean Conference on Control and Systems. IEEE, 1997.
[2] 陈宁, 彭俊洁, 王磊,等. 模糊灰色认知网络的建模方法及应用[J]. 自动化学报, 2018, v.44(07):77-86.
[3] Elpiniki Papageorgiou, Chrysostomos Stylios, Peter Groumpos. Fuzzy Cognitive Map Learning Based on Nonlinear Hebbian Rule[M]// AI 2003: Advances in Artificial Intelligence. Springer Berlin Heidelberg, 2003.
[4] Neural Networks and Fuzzy Systems课程ppt