RSA知识点总结

发表于 | 更新于: | 分类于 | 本文总阅读量 次
字数统计: 4.1k | 阅读时长 ≈ 20

大数分解

大数分解网页

http://www.factordb.com/index.php

yafu

  1. 运行yafu-x64.exe，在窗口中输入factor(n)，n即为待分解的大数。
  2. 在factor.log中找到分解结果。

利用z3解方程

可以加快解题速度，此处以一个简单的例子展示如何用z3解方程（首先需要安装z3和z3-solver）。
$\begin{cases}\ x1+x2=3\\ x1-x2=-1\end{cases}$

1
2
3
4
5
6
7
8
9
from z3 import *

x1 = Int('x1')
x2 = Int('x2')
s = Solver()
s.add(x1 + x2 == 3)
s.add(x1 - x2 == -1)
if s.check()==sat:
    print(s.model())

如例题[GWCTF 2019]BabyRSA

已知p,q,e求d

方法一：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
p=473398607161
q=4511491
e=17
n = (p-1) * (q-1)

def extendedEuclid(a, b):
    if b == 0:
        return 1, 0
    else:
        x, y= extendedEuclid(b, a % b)
        x, y = y, (x - (a // b) * y)
        return x, y
d = extendedEuclid(e,n)[0]
print(d)

方法二(常用，gmpy2库)：

1
2
3
4
# 已知e,p,q
import gmpy2
phin = (p-1) * (q-1)
d = gmpy2.invert(e,phin)

方法三(sage)：

1
2
phin = (p-1) * (q-1)
d = inverse_mod(e,phin)

已知n,dp,e求d

相关例题如：Buuoj RSA2

  1. 要先根据e,dp求p。首先
      $dp\ =\ d\ mod\ (p-1)$
      $ed\ \equiv\ 1\ mod\ \phi(n)$
    而$\phi(n)\ =\ (p-1)(q-1)$，所以有
      $ed\ =\ 1+x(p-1)(q-1)$
      $edp\ mod\ (p-1)\ \equiv\ ed\ mod\ (p-1)$
    进而：
      $edp\ =\ ed+y(p-1)$
      $edp\ =\ 1+x(p-1)(q-1)+y(p-1)$
    因此可整理为：
      $edp\ =\ 1+y(p-1)$
    又有$dp\ \lt\ p-1$，所以$e\ \gt\ y$。从1到e遍历即可求得正确的y，进而得到正确的p值。得到p后可有已知的n求得q，进而回到已知$e$和$\phi(n)$求解$d$的问题。得到代码如下，注意求p时是整型除法，否则会在n%p时报溢出错误： 
1
2
3
4
5
6
for y in range(1,e):
    if (e*dp - 1)%y == 0:
        p = (e*dp - 1)//y + 1
        if n%p == 0:
            print(p)
            break

小指数明文爆破

相关例题，Buuoj Dangerous RSA

  1. 题目已知条件有n,e,c其中e是非常小的值，比如3。RSA的加密过程为$c=m^e\ mod\ n$。
    如果m很小，n很大，也即可能是以下情况$^{[2]}$：
      $m^e\ \lt\ n$
    此时，$c=m^e$，开e次根即可得到m。
    如果，$m^e \gt\ n$但是并未超过n太多，又由于对c我们可能有$m^e=c+kn$，所以可以得到以下的表达式：
      $m=\sqrt[e]{c+kn}$
    这样我们可以通过爆破k的大小来求解明文了。
  2. 基本代码如下： 
1
2
3
4
5
6
7
8
9
# 已知n,e,c
import gmpy2
from Crypto.Util.number import long_to_bytes
k = 0
while 1:
    if gmpy2.iroot(c+k*n,e)[1]==1:
        print(long_to_bytes(gmpy2.iroot(c+k*n,e)[0]))
        break
    k += 1

iroot(c+k*n,e)函数就是在计算$\sqrt[e]{c+kn}$，其返回结果第一个元素为计算结果，第二个元素是表示结果是否精确的布尔值

分数，求导

相关例题：[BJDCTF2020]easyrsa

分数

1
2
3
# Fraction(8, 6) will produce a rational number equivalent to 4/3, Both arguments must be Rational. The numerator defaults to 0 and the denominator defaults to 1 so that Fraction(3) == 3 and Fraction() == 0.
from fractions import Fraction
x = Fraction(8,6)

求导

http://liao.cpython.org/scipy17/
如对$arctan(p)$求导（p为变量） 

1
2
from sympy import Derivative
x = Derivative(arctan(p),p)

已知e,n且e很大时求d: RSA Wiener Attack 维纳攻击

参考：https://github.com/pablocelayes/rsa-wiener-attack
求d的方法： 

1
2
from RSAwienerHacker import hack_RSA
d = hack_RSA(e,n)

相关例题Buuoj rsa2

openssl

  1. 首先需要下载安装openssl，下载地址
  2. 将其bin目录添加到系统变量path中
  3. 基本用法参考https://www.cnblogs.com/wyzhou/p/9738964.html
  4. 如利用openssl从文件获取公钥信息（不输出文件）：openssl rsa -pubin -in key.pub -text -noout

利用Crypto.PublicKey的RSA模块从文件中获取公钥信息n,e

这个文件可能是二进制文件，key.pub，pub.key等形式

1
2
3
4
from Crypto.PublicKey import RSA
f = open("key.pub","rb").read()
pub = RSA.importKey(f)
print(pub.n,pub.e)

相关例题：Buuoj RSA, 攻防世界 cr4-poor-rsa

已知e,d的值和p,q的位数，求p,q的值

先验知识：
  $n=pq$
  $\phi(n)=(p-1)(q-1)$
  $ed\equiv1\ mod\ \phi(n)$
所以，大概有

如果我们已知p,q的位数，那就大概知道n的位数，$\phi(n)$的位数与n差别不大。同时$ed-1$的位数可以通过其值得到范围，因此我们可以通过$\frac{(ed-1)的位数}{\phi(n)的位数}$大致确定x的位数，随即可以在此范围遍历得到素数p,q的值。
相关例题：[NCTF2019]babyRSA

已知多组n,c的值

中国剩余定理

参考代码

遍历n，看有无非1的公因数，其值即为p或q的值

RsaCtfTool

源代码

  1. 安装过程中注意mpfr和mpc都应从官网确认最新版本后再下载对应版本并安装。
  2. 使用方法：

已知n的值，且p，q大小相近，如何求出p和q

  1. 先对n求平方根，得到一个和p值相近的值，再求其临近的素数，即为p值
  2. q = n // p 
1
2
3
near_p = isqrt(n)
p = next_prime(near_p)
q = n // p

已知dp,dq,p,q,c求明文

参考 

1
2
3
4
5
6
7
8
9
10
import gmpy2
import binascii


def decrypt(dp, dq, p, q, c):
    InvQ = gmpy2.invert(q, p)
    mp = pow(c, dp, p)
    mq = pow(c, dq, q)
    m = (((mp-mq)*InvQ) % p)*q+mq
    print(binascii.unhexlify(hex(m)[2:]))

例题

Buuoj RSA

解法一

  1. 给了flag.enc和pub.key文件，其中pub.key文件存放了公钥信息，这是个ASCII文本文件可直接用记事本打开。得到以下信息： 

    1
    2
    3
    4
    -----BEGIN PUBLIC KEY-----
    MDwwDQYJKoZIhvcNAQEBBQADKwAwKAIhAMAzLFxkrkcYL2wch21CM2kQVFpY9+7+
    /AvKr1rzQczdAgMBAAE=
    -----END PUBLIC KEY-----

  2. 借助RSA密钥解析网站解析密钥指数和模数信息，得以下结果： 

1
2
3
key长度：256
模数：C0332C5C64AE47182F6C1C876D42336910545A58F7EEFEFC0BCAAF5AF341CCDD
指数：65537

  1. 用Python得到n的十进制形式 

    1
    2
    n = '0xC0332C5C64AE47182F6C1C876D42336910545A58F7EEFEFC0BCAAF5AF341CCDD'
    n = int(n,16)

  2. 得到n=86934482296048119190666062003494800588905656017203025617216654058378322103517，放到大数分解网站分解。得到： 

1
2
p=285960468890451637935629440372639283459
q=304008741604601924494328155975272418463
  1. 利用gmpy2库求解d，由以上已得数据有以下代码d = gmpy2.invert(e,(p-1)*(q-1))，得到： 
1
d=81176168860169991027846870170527607562179635470395365333547868786951080991441

注意这个invert函数的用法：
invert(x, m) Return y such that x*y == 1 (mod m).

  1. 最后从flag.enc文件中获取flag 
1
2
3
4
5
import rsa
k = rsa.PrivateKey(n,e,int(d),p,q)
f = open("flag.enc","rb+").read()
flag = rsa.decrypt(f,k)
print(flag)

flag{decrypt_256}

或者参考 

1
2
3
4
5
6
7
8
9
from Crypto.PublicKey import RSA
from Crypto.Cipher import PKCS1_OAEP
from base64 import b64decode
key_info = RSA.construct((n, e, d, p, q))
key = RSA.importKey(key_info.exportKey())
key = PKCS1_OAEP.new(key)
c = open('flag.enc', 'r').read()
flag = key.decrypt(c)
print(flag)

注意这个rsa.PrivateKey所有的参数都要是int

解法二

主要是获取n,e的方法不同： 

1
2
3
4
5
from Crypto.PublicKey import RSA

f = open("pub.key","rb").read()
pub = RSA.importKey(f)
print(pub.n,pub.e)

直接输出86934482296048119190666062003494800588905656017203025617216654058378322103517 65537

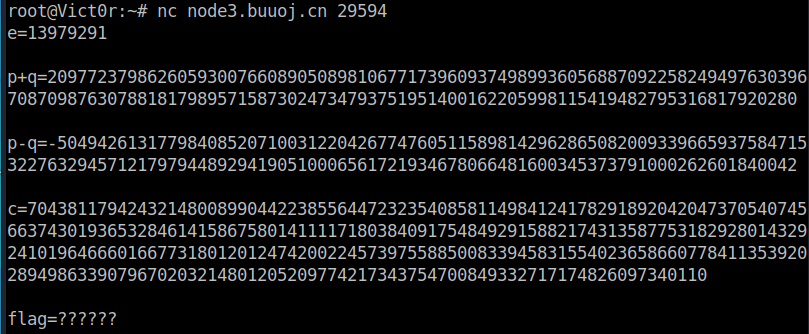
BJDCTF 2nd rsa0

  1. 给了node3.buuoj.cn:29594，nc连接，得到
    1931211-20200729165149511-1880562176
1
2
3
4
e = 13979291
p+q = 20977237986260593007660890508981067717396093749899360568870922582494976303967087098763078818179895715873024734793751951400162205998115419482795316817920280
p-q = -5049426131779840852071003122042677476051158981429628650820093396659375847153227632945712179794489294190510006561721934678066481600345373791000262601840042
c = 70438117942432148008990442238556447232354085811498412417829189204204737054074566374301936532846141586758014111171803840917548492915882174313587753182928014329241019646660166773180120124742002245739755885008339458315540236586607784113539202894986339079670203214801205209774217343754700849332717174826097340110
  1. Python代码如下： 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
import gmpy2
from Crypto.Util.number import long_to_bytes

p_add_q = 20977237986260593007660890508981067717396093749899360568870922582494976303967087098763078818179895715873024734793751951400162205998115419482795316817920280
p_sub_q = -5049426131779840852071003122042677476051158981429628650820093396659375847153227632945712179794489294190510006561721934678066481600345373791000262601840042
c = 70438117942432148008990442238556447232354085811498412417829189204204737054074566374301936532846141586758014111171803840917548492915882174313587753182928014329241019646660166773180120124742002245739755885008339458315540236586607784113539202894986339079670203214801205209774217343754700849332717174826097340110
p = (p_add_q + p_sub_q)//2
q = (p_add_q - p_sub_q)//2
phn = (p - 1) * (q - 1)
e = 13979291
d = gmpy2.invert(e,phn)
n = p * q
m = pow(c,int(d),n)
print(long_to_bytes(m))

flag{2824f2c0-b958-4d96-9ce7-1b3d40e9333d}

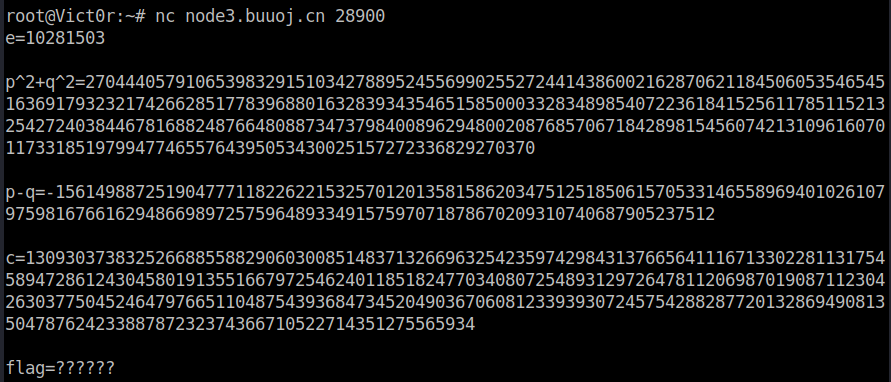
BJDCTF 2nd rsa1

  1. nc node3.buuoj.cn 28900得到：
    1931211-20200729173057340-1474699671
1
2
3
4
e = 10281503
p^2 + q^2 = 270444057910653983291510342788952455699025527244143860021628706211845060535465451636917932321742662851778396880163283934354651585000332834898540722361841525611785115213254272403844678168824876648088734737984008962948002087685706718428981545607421310961607011733185197994774655764395053430025157272336829270370
p - q=-1561498872519047771182262215325701201358158620347512518506157053314655896940102610797598167661629486698972575964893349157597071878670209310740687905237512
c = 130930373832526688558829060300851483713266963254235974298431376656411167133022811317545894728612430458019135516679725462401185182477034080725489312972647811206987019087112304263037750452464797665110487543936847345204903670608123393930724575428828772013286949081350478762423388787232374366710522714351275565934
  1. 根据pq的信息解方程即可，$2(p^2 + q^2) - (p-q)^2 = (p+q)^2$，emmm想用Python的cmath开根号或pow时会报溢出，所以整个解题过程在sage中实现。
  2. sage代码如下： 
1
2
3
4
5
6
7
8
9
10
11
12
13
import binascii
x = 270444057910653983291510342788952455699025527244143860021628706211845060535465451636917932321742662851778396880163283934354651585000332834898540722361841525611785115213254272403844678168824876648088734737984008962948002087685706718428981545607421310961607011733185197994774655764395053430025157272336829270370
p_sub_q = -1561498872519047771182262215325701201358158620347512518506157053314655896940102610797598167661629486698972575964893349157597071878670209310740687905237512
p_add_q = sqrt(2*x-pow(p_sub_q,2))
p = (p_add_q + p_sub_q)//2
q = (p_add_q - p_sub_q)//2
phn = (p - 1) * (q - 1)
e = 10281503
d = inverse_mod(e,phn)
n = p * q
c = 130930373832526688558829060300851483713266963254235974298431376656411167133022811317545894728612430458019135516679725462401185182477034080725489312972647811206987019087112304263037750452464797665110487543936847345204903670608123393930724575428828772013286949081350478762423388787232374366710522714351275565934
m=pow(c,d,n)
print(binascii.unhexlify(hex(m)[2:]))

flag{795faee7-4d4b-432c-9796-4758027c8a58}

RSAROLL

  1. data.txt中的数据如下： 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
{920139713,19}  

704796792
752211152
274704164
18414022
368270835
483295235
263072905
459788476
483295235
459788476
663551792
475206804
459788476
428313374
475206804
459788476
425392137
704796792
458265677
341524652
483295235
534149509
425392137
428313374
425392137
341524652
458265677
263072905
483295235
828509797
341524652
425392137
475206804
428313374
483295235
475206804
459788476
306220148
  1. 把920139713拿到大数分解网站分解，发现可以分解成18443和49891。所以{920139713,19}应该是{n,e}，剩下的行是密文。需要做的是循环求解每行的明文。
  2. 逻辑比较简单。先由分解得到的p和q，以及已知的e求得d，然后读取data.txt中的内容，循环求解明文。代码如下： 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
import gmpy2

n = 920139713
e = 19
p = 18443
q = 49891
d = gmpy2.invert(e,(p-1)*(q-1))
f = open("data.txt","r")
flag = ""
for line in f.readlines()[2:]:
    # 从第三行开始读
    c = int(line)
    flag += chr(pow(c,d,n))
print(flag)
f.close()

flag{13212je2ue28fy71w8u87y31r78eu1e2}

[HDCTF2019]basic rsa

  1. 题目attachment.py，具体代码如下： 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
import gmpy2
from Crypto.Util.number import *
from binascii import a2b_hex,b2a_hex

flag = "*****************"

p = 262248800182277040650192055439906580479
q = 262854994239322828547925595487519915551

e = 65533
n = p*q


c = pow(int(b2a_hex(flag),16),e,n)

print c

# 27565231154623519221597938803435789010285480123476977081867877272451638645710
  1. 所以基本逻辑很简单，先通过p，q，e求d，上文已经有求解方法和案例。然后利用c，d，n求int(b2a_hex(flag),16)再反求flag。解题代码如下： 
1
2
3
4
5
6
7
8
9
10
11
12
import gmpy2
from binascii import a2b_hex

p = 262248800182277040650192055439906580479
q = 262854994239322828547925595487519915551
e = 65533
c = 27565231154623519221597938803435789010285480123476977081867877272451638645710
d = gmpy2.invert(e,(p-1)*(q-1))
m = pow(c,d,p*q)
print(m)
flag = a2b_hex(hex(m)[2:])
print(flag)

注意这里m从10进制转到16进制后，前面会有0x的前缀，所以取下标2及以后部分。flag{B4by_Rs4}

[GUET-CTF2019]BabyRSA

  1. 题目给了一个BabyRsa文件，用winhex打开发现这是一个文本文件，直接用记事本打开即可。有以下信息： 
1
2
3
4
5
p + q : 0x1232fecb92adead91613e7d9ae5e36fe6bb765317d6ed38ad890b4073539a6231a6620584cea5730b5af83a3e80cf30141282c97be4400e33307573af6b25e2ea
(p+1)(q+1) : 0x5248becef1d925d45705a7302700d6a0ffe5877fddf9451a9c1181c4d82365806085fd86fbaab08b6fc66a967b2566d743c626547203b34ea3fdb1bc06dd3bb765fd8b919e3bd2cb15bc175c9498f9d9a0e216c2dde64d81255fa4c05a1ee619fc1fc505285a239e7bc655ec6605d9693078b800ee80931a7a0c84f33c851740
e : 0xe6b1bee47bd63f615c7d0a43c529d219
d : 0x2dde7fbaed477f6d62838d55b0d0964868cf6efb2c282a5f13e6008ce7317a24cb57aec49ef0d738919f47cdcd9677cd52ac2293ec5938aa198f962678b5cd0da344453f521a69b2ac03647cdd8339f4e38cec452d54e60698833d67f9315c02ddaa4c79ebaa902c605d7bda32ce970541b2d9a17d62b52df813b2fb0c5ab1a5
enc_flag : 0x50ae00623211ba6089ddfae21e204ab616f6c9d294e913550af3d66e85d0c0693ed53ed55c46d8cca1d7c2ad44839030df26b70f22a8567171a759b76fe5f07b3c5a6ec89117ed0a36c0950956b9cde880c575737f779143f921d745ac3bb0e379c05d9a3cc6bf0bea8aa91e4d5e752c7eb46b2e023edbc07d24a7c460a34a9a
  1. 所以令x=p+q，y=(p+1)(q+1)，就有n=p*q=y-x-1，这里给的e其实用不到。直接m=pow(enc_flag,d,n)就得到明文数据了，解题代码如下： 
1
2
3
4
5
6
7
8
9
10
11
12
from Crypto.Util.number import long_to_bytes
# x = p+q
# y = (p+1)(q+1)

x = 0x1232fecb92adead91613e7d9ae5e36fe6bb765317d6ed38ad890b4073539a6231a6620584cea5730b5af83a3e80cf30141282c97be4400e33307573af6b25e2ea
y = 0x5248becef1d925d45705a7302700d6a0ffe5877fddf9451a9c1181c4d82365806085fd86fbaab08b6fc66a967b2566d743c626547203b34ea3fdb1bc06dd3bb765fd8b919e3bd2cb15bc175c9498f9d9a0e216c2dde64d81255fa4c05a1ee619fc1fc505285a239e7bc655ec6605d9693078b800ee80931a7a0c84f33c851740
d = 0x2dde7fbaed477f6d62838d55b0d0964868cf6efb2c282a5f13e6008ce7317a24cb57aec49ef0d738919f47cdcd9677cd52ac2293ec5938aa198f962678b5cd0da344453f521a69b2ac03647cdd8339f4e38cec452d54e60698833d67f9315c02ddaa4c79ebaa902c605d7bda32ce970541b2d9a17d62b52df813b2fb0c5ab1a5
enc_flag = 0x50ae00623211ba6089ddfae21e204ab616f6c9d294e913550af3d66e85d0c0693ed53ed55c46d8cca1d7c2ad44839030df26b70f22a8567171a759b76fe5f07b3c5a6ec89117ed0a36c0950956b9cde880c575737f779143f921d745ac3bb0e379c05d9a3cc6bf0bea8aa91e4d5e752c7eb46b2e023edbc07d24a7c460a34a9a

n = y - x - 1
m = pow(enc_flag,d,n)
print(long_to_bytes(m))

flag{cc7490e-78ab-11e9-b422-8ba97e5da1fd}

Buuoj RSA2

  1. 题目信息： 
1
2
3
4
e = 65537
n = 248254007851526241177721526698901802985832766176221609612258877371620580060433101538328030305219918697643619814200930679612109885533801335348445023751670478437073055544724280684733298051599167660303645183146161497485358633681492129668802402065797789905550489547645118787266601929429724133167768465309665906113
dp = 905074498052346904643025132879518330691925174573054004621877253318682675055421970943552016695528560364834446303196939207056642927148093290374440210503657
c = 140423670976252696807533673586209400575664282100684119784203527124521188996403826597436883766041879067494280957410201958935737360380801845453829293997433414188838725751796261702622028587211560353362847191060306578510511380965162133472698713063592621028959167072781482562673683090590521214218071160287665180751
  1. 这是由dp求解p的问题。求解方法已在上文中有具体推导过程，解题代码如下： 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
import gmpy2
from Crypto.Util.number import long_to_bytes

e = 65537
n = 248254007851526241177721526698901802985832766176221609612258877371620580060433101538328030305219918697643619814200930679612109885533801335348445023751670478437073055544724280684733298051599167660303645183146161497485358633681492129668802402065797789905550489547645118787266601929429724133167768465309665906113
dp = 905074498052346904643025132879518330691925174573054004621877253318682675055421970943552016695528560364834446303196939207056642927148093290374440210503657
c = 140423670976252696807533673586209400575664282100684119784203527124521188996403826597436883766041879067494280957410201958935737360380801845453829293997433414188838725751796261702622028587211560353362847191060306578510511380965162133472698713063592621028959167072781482562673683090590521214218071160287665180751

p = 0
for y in range(1,e):
    if (e*dp - 1)%y == 0:
        p = (e*dp - 1)//y + 1
        if n%p == 0:
            print(p)
            break
q = n // p
print(q)

d = gmpy2.invert(e,(p-1)*(q-1))
m = pow(c,d,n)
print(long_to_bytes(m))

flag{wow_leaking_dp_breaks_rsa?_98924743502}

Buuoj Dangerous RSA

  1. 题目提供的信息： 
1
2
3
4
n:  0x52d483c27cd806550fbe0e37a61af2e7cf5e0efb723dfc81174c918a27627779b21fa3c851e9e94188eaee3d5cd6f752406a43fbecb53e80836ff1e185d3ccd7782ea846c2e91a7b0808986666e0bdadbfb7bdd65670a589a4d2478e9adcafe97c6ee23614bcb2ecc23580f4d2e3cc1ecfec25c50da4bc754dde6c8bfd8d1fc16956c74d8e9196046a01dc9f3024e11461c294f29d7421140732fedacac97b8fe50999117d27943c953f18c4ff4f8c258d839764078d4b6ef6e8591e0ff5563b31a39e6374d0d41c8c46921c25e5904a817ef8e39e5c9b71225a83269693e0b7e3218fc5e5a1e8412ba16e588b3d6ac536dce39fcdfce81eec79979ea6872793L
e:  0x3
c:0x10652cdfaa6b63f6d7bd1109da08181e500e5643f5b240a9024bfa84d5f2cac9310562978347bb232d63e7289283871efab83d84ff5a7b64a94a79d34cfbd4ef121723ba1f663e514f83f6f01492b4e13e1bb4296d96ea5a353d3bf2edd2f449c03c4a3e995237985a596908adc741f32365
so,how to get the message?
  1. 小指数明文爆破，前文已有原理。具体解题代码如下： 
1
2
3
4
5
6
7
8
9
10
11
12
13
import gmpy2
from Crypto.Util.number import long_to_bytes

n = 0x52d483c27cd806550fbe0e37a61af2e7cf5e0efb723dfc81174c918a27627779b21fa3c851e9e94188eaee3d5cd6f752406a43fbecb53e80836ff1e185d3ccd7782ea846c2e91a7b0808986666e0bdadbfb7bdd65670a589a4d2478e9adcafe97c6ee23614bcb2ecc23580f4d2e3cc1ecfec25c50da4bc754dde6c8bfd8d1fc16956c74d8e9196046a01dc9f3024e11461c294f29d7421140732fedacac97b8fe50999117d27943c953f18c4ff4f8c258d839764078d4b6ef6e8591e0ff5563b31a39e6374d0d41c8c46921c25e5904a817ef8e39e5c9b71225a83269693e0b7e3218fc5e5a1e8412ba16e588b3d6ac536dce39fcdfce81eec79979ea6872793
e = 0x3
c = 0x10652cdfaa6b63f6d7bd1109da08181e500e5643f5b240a9024bfa84d5f2cac9310562978347bb232d63e7289283871efab83d84ff5a7b64a94a79d34cfbd4ef121723ba1f663e514f83f6f01492b4e13e1bb4296d96ea5a353d3bf2edd2f449c03c4a3e995237985a596908adc741f32365

k = 0
while 1:
    if gmpy2.iroot(c+k*n,e)[1]==1:
        print(long_to_bytes(gmpy2.iroot(c+k*n,e)[0]))
        break
    k += 1

flag{25df8caf006ee5db94d48144c33b2c3b}

[GWCTF 2019]BabyRSA

  1. 解压缩文件，有encrypt.py和secret，其中secret是文本文件，内容如下： 
1
2
3
N=636585149594574746909030160182690866222909256464847291783000651837227921337237899651287943597773270944384034858925295744880727101606841413640006527614873110651410155893776548737823152943797884729130149758279127430044739254000426610922834573094957082589539445610828279428814524313491262061930512829074466232633130599104490893572093943832740301809630847541592548921200288222432789208650949937638303429456468889100192613859073752923812454212239908948930178355331390933536771065791817643978763045030833712326162883810638120029378337092938662174119747687899484603628344079493556601422498405360731958162719296160584042671057160241284852522913676264596201906163
m1=90009974341452243216986938028371257528604943208941176518717463554774967878152694586469377765296113165659498726012712288670458884373971419842750929287658640266219686646956929872115782173093979742958745121671928568709468526098715927189829600497283118051641107305128852697032053368115181216069626606165503465125725204875578701237789292966211824002761481815276666236869005129138862782476859103086726091860497614883282949955023222414333243193268564781621699870412557822404381213804026685831221430728290755597819259339616650158674713248841654338515199405532003173732520457813901170264713085107077001478083341339002069870585378257051150217511755761491021553239
m2=487443985757405173426628188375657117604235507936967522993257972108872283698305238454465723214226871414276788912058186197039821242912736742824080627680971802511206914394672159240206910735850651999316100014691067295708138639363203596244693995562780286637116394738250774129759021080197323724805414668042318806010652814405078769738548913675466181551005527065309515364950610137206393257148357659666687091662749848560225453826362271704292692847596339533229088038820532086109421158575841077601268713175097874083536249006018948789413238783922845633494023608865256071962856581229890043896939025613600564283391329331452199062858930374565991634191495137939574539546

encrypt.py如下： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
import hashlib
import sympy
from Crypto.Util.number import *

flag = 'GWHT{******}'
secret = '******'

assert(len(flag) == 38)

half = len(flag) / 2

flag1 = flag[:half]
flag2 = flag[half:]

secret_num = getPrime(1024) * bytes_to_long(secret)

p = sympy.nextprime(secret_num)
q = sympy.nextprime(p)

N = p * q

e = 0x10001

F1 = bytes_to_long(flag1)
F2 = bytes_to_long(flag2)

c1 = F1 + F2
c2 = pow(F1, 3) + pow(F2, 3)
assert(c2 < N)

m1 = pow(c1, e, N)
m2 = pow(c2, e, N)

output = open('secret', 'w')
output.write('N=' + str(N) + '\n')
output.write('m1=' + str(m1) + '\n')
output.write('m2=' + str(m2) + '\n')
output.close()
  1. 由以上代码可以得到以下表达式：
    $c1=F1+F2$
    $c2=F1^{3}+F2^{3}$
    $c1=m1^{d}\ mod\ N$
    $c2=m2^{d}\ mod\ N$
    d可由e,p,q求得。而p,q可通过yafu对N进行分解得到。所以拿到d后就可以求出c1和c2，然后解方程即可得到F1和F2，最后拼出flag。
  2. 解题代码如下： 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
from Crypto.Util.number import long_to_bytes
from z3 import *
from gmpy2 import invert

N = 636585149594574746909030160182690866222909256464847291783000651837227921337237899651287943597773270944384034858925295744880727101606841413640006527614873110651410155893776548737823152943797884729130149758279127430044739254000426610922834573094957082589539445610828279428814524313491262061930512829074466232633130599104490893572093943832740301809630847541592548921200288222432789208650949937638303429456468889100192613859073752923812454212239908948930178355331390933536771065791817643978763045030833712326162883810638120029378337092938662174119747687899484603628344079493556601422498405360731958162719296160584042671057160241284852522913676264596201906163
p = 797862863902421984951231350430312260517773269684958456342860983236184129602390919026048496119757187702076499551310794177917920137646835888862706126924088411570997141257159563952725882214181185531209186972351469946269508511312863779123205322378452194261217016552527754513215520329499967108196968833163329724620251096080377748737
q = 797862863902421984951231350430312260517773269684958456342860983236184129602390919026048496119757187702076499551310794177917920137646835888862706126924088411570997141257159563952725882214181185531209186972351469946269508511312863779123205322378452194261217016552527754513215520329499967108196968833163329724620251096080377747699

m1 = 90009974341452243216986938028371257528604943208941176518717463554774967878152694586469377765296113165659498726012712288670458884373971419842750929287658640266219686646956929872115782173093979742958745121671928568709468526098715927189829600497283118051641107305128852697032053368115181216069626606165503465125725204875578701237789292966211824002761481815276666236869005129138862782476859103086726091860497614883282949955023222414333243193268564781621699870412557822404381213804026685831221430728290755597819259339616650158674713248841654338515199405532003173732520457813901170264713085107077001478083341339002069870585378257051150217511755761491021553239
m2 = 487443985757405173426628188375657117604235507936967522993257972108872283698305238454465723214226871414276788912058186197039821242912736742824080627680971802511206914394672159240206910735850651999316100014691067295708138639363203596244693995562780286637116394738250774129759021080197323724805414668042318806010652814405078769738548913675466181551005527065309515364950610137206393257148357659666687091662749848560225453826362271704292692847596339533229088038820532086109421158575841077601268713175097874083536249006018948789413238783922845633494023608865256071962856581229890043896939025613600564283391329331452199062858930374565991634191495137939574539546

phn = (p-1) * (q-1)
e = 0x10001
d = invert(e,phn)
c1 = pow(m1,d,N)
c2 = pow(m2,d,N)
print("c1 =",c1)
print("c2 =",c2)

F1 = Int('F1')
F2 = Int('F2')
s = Solver()
s.add(F1 + F2 == int(c1))
s.add(F1**3 + F2**3 == int(c2))
if s.check()==sat:
    print(s.model())
print(long_to_bytes(1590956290598033029862556611630426044507841845)+long_to_bytes(1141553212031156130619789508463772513350070909))

GWHT{f709e0e2cfe7e530ca8972959a1033b2}

[HDCTF2019]bbbbbbrsa

  1. 题目给了enc和encode.py，内容如下： 
1
2
3
p = 177077389675257695042507998165006460849
n = 37421829509887796274897162249367329400988647145613325367337968063341372726061
c = ==gMzYDNzIjMxUTNyIzNzIjMyYTM4MDM0gTMwEjNzgTM2UTN4cjNwIjN2QzM5ADMwIDNyMTO4UzM2cTM5kDN2MTOyUTO5YDM0czM3MjM
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
from base64 import b64encode as b32encode
from gmpy2 import invert,gcd,iroot
from Crypto.Util.number import *
from binascii import a2b_hex,b2a_hex
import random

flag = "******************************"

nbit = 128

p = getPrime(nbit)
q = getPrime(nbit)
n = p*q

print p
print n

phi = (p-1)*(q-1)

e = random.randint(50000,70000)

while True:
	if gcd(e,phi) == 1:
		break;
	else:
		e -= 1;

c = pow(int(b2a_hex(flag),16),e,n)

print b32encode(str(c))[::-1]

# 2373740699529364991763589324200093466206785561836101840381622237225512234632
  1. 所以思路是：先求c，这个c值不看代码，直接从enc文本中就可以看出是逆序的base64结果，所以先逆序过来再base64解密即可；其次，由e爆破得到d；最后因为有$c=int(b2a_hex(flag),16)^{e}\ mod\ n$，所以有$int(b2a_hex(flag),16)=c^{d}\ mod\ n$，可整理得到flag，代码如下： 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
from gmpy2 import invert,gcd
import base64
from Crypto.Util.number import long_to_bytes

p = 177077389675257695042507998165006460849
n = 37421829509887796274897162249367329400988647145613325367337968063341372726061
c = "==gMzYDNzIjMxUTNyIzNzIjMyYTM4MDM0gTMwEjNzgTM2UTN4cjNwIjN2QzM5ADMwIDNyMTO4UzM2cTM5kDN2MTOyUTO5YDM0czM3MjM"

q = n // p

c = str(c)[::-1]
c = base64.b64decode(c)
# c = 2373740699529364991763589324200093466206785561836101840381622237225512234632
print(c)

phi = (p-1) * (q-1)

for e in range(50000,70000):
    if gcd(e,phi) == 1:
        d = invert(e,phi)
        x = pow(int(c),int(d),n)
        flag = str(long_to_bytes(x))
        if "flag" in flag or "CTF" in flag or "ctf" in flag:
            print(flag)

flag{rs4_1s_s1mpl3!#}

[BJDCTF2020]easyrsa

  1. 题目给了rsa_task.py，具体如下： 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
from Crypto.Util.number import getPrime,bytes_to_long
from sympy import Derivative
from fractions import Fraction
from secret import flag

p=getPrime(1024)
q=getPrime(1024)
e=65537
n=p*q
z=Fraction(1,Derivative(arctan(p),p))-Fraction(1,Derivative(arth(q),q))
m=bytes_to_long(flag)
c=pow(m,e,n)
print(c,z,n)
'''
output:
7922547866857761459807491502654216283012776177789511549350672958101810281348402284098310147796549430689253803510994877420135537268549410652654479620858691324110367182025648788407041599943091386227543182157746202947099572389676084392706406084307657000104665696654409155006313203957292885743791715198781974205578654792123191584957665293208390453748369182333152809882312453359706147808198922916762773721726681588977103877454119043744889164529383188077499194932909643918696646876907327364751380953182517883134591810800848971719184808713694342985458103006676013451912221080252735948993692674899399826084848622145815461035
32115748677623209667471622872185275070257924766015020072805267359839059393284316595882933372289732127274076434587519333300142473010344694803885168557548801202495933226215437763329280242113556524498457559562872900811602056944423967403777623306961880757613246328729616643032628964072931272085866928045973799374711846825157781056965164178505232524245809179235607571567174228822561697888645968559343608375331988097157145264357626738141646556353500994924115875748198318036296898604097000938272195903056733565880150540275369239637793975923329598716003350308259321436752579291000355560431542229699759955141152914708362494482
15310745161336895413406690009324766200789179248896951942047235448901612351128459309145825547569298479821101249094161867207686537607047447968708758990950136380924747359052570549594098569970632854351825950729752563502284849263730127586382522703959893392329333760927637353052250274195821469023401443841395096410231843592101426591882573405934188675124326997277775238287928403743324297705151732524641213516306585297722190780088180705070359469719869343939106529204798285957516860774384001892777525916167743272419958572055332232056095979448155082465977781482598371994798871917514767508394730447974770329967681767625495394441
'''

  1. 所以基本思路是由z求出p和q，再有p,q,e得到d，由c,d,n求m即可得到最终的flag

  2. 由z求p,q。首先$z=\frac{1}{arctan’(p)}\ -\ \frac{1}{arth’(q)}$，其中$arctan’(p)=\frac{1}{1+p^{2}}$，$arth’(q)=\frac{1}{1-q^{2}}$，因此有$z=p^{2}+q^{2}$。同时我们已知有$n=pq$，z和n的值已知，利用z3库联立解方程即可。代码如下： 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
from z3 import *

# z = p^2 + q^2
# n = p * q
z = 32115748677623209667471622872185275070257924766015020072805267359839059393284316595882933372289732127274076434587519333300142473010344694803885168557548801202495933226215437763329280242113556524498457559562872900811602056944423967403777623306961880757613246328729616643032628964072931272085866928045973799374711846825157781056965164178505232524245809179235607571567174228822561697888645968559343608375331988097157145264357626738141646556353500994924115875748198318036296898604097000938272195903056733565880150540275369239637793975923329598716003350308259321436752579291000355560431542229699759955141152914708362494482
n = 15310745161336895413406690009324766200789179248896951942047235448901612351128459309145825547569298479821101249094161867207686537607047447968708758990950136380924747359052570549594098569970632854351825950729752563502284849263730127586382522703959893392329333760927637353052250274195821469023401443841395096410231843592101426591882573405934188675124326997277775238287928403743324297705151732524641213516306585297722190780088180705070359469719869343939106529204798285957516860774384001892777525916167743272419958572055332232056095979448155082465977781482598371994798871917514767508394730447974770329967681767625495394441

p = Int('p')
q = Int('q')
s = Solver()
s.add(p**2 + q**2 == z)
s.add(p*q == n)
if s.check()==sat:
    print(s.model())

最终输出可得： 

1
2
p = 144564833334456076455156647979862690498796694770100520405218930055633597500009574663803955456004439398699669751249623406199542605271188909145969364476344963078599240058180033000440459281558347909876143313940657252737586803051935392596519226965519859474501391969755712097119163926672753588797180811711004203301
q = 105909195259921349656664570904199242969110902804477734660927330311460997899731622163728968380757294196277263615386525795293086103142131020215128282050307177125962302515483190468569376643751587606016315185736245896434947691528567696271911398179288329609207435393579332931583829355558784305002360873458907029141
  1. 由p,q,e,c,n求m，并得到flag 
1
2
3
4
5
6
7
8
9
10
11
from Crypto.Util.number import *
from gmpy2 import invert

c = 7922547866857761459807491502654216283012776177789511549350672958101810281348402284098310147796549430689253803510994877420135537268549410652654479620858691324110367182025648788407041599943091386227543182157746202947099572389676084392706406084307657000104665696654409155006313203957292885743791715198781974205578654792123191584957665293208390453748369182333152809882312453359706147808198922916762773721726681588977103877454119043744889164529383188077499194932909643918696646876907327364751380953182517883134591810800848971719184808713694342985458103006676013451912221080252735948993692674899399826084848622145815461035
n = 15310745161336895413406690009324766200789179248896951942047235448901612351128459309145825547569298479821101249094161867207686537607047447968708758990950136380924747359052570549594098569970632854351825950729752563502284849263730127586382522703959893392329333760927637353052250274195821469023401443841395096410231843592101426591882573405934188675124326997277775238287928403743324297705151732524641213516306585297722190780088180705070359469719869343939106529204798285957516860774384001892777525916167743272419958572055332232056095979448155082465977781482598371994798871917514767508394730447974770329967681767625495394441
e = 65537
p = 144564833334456076455156647979862690498796694770100520405218930055633597500009574663803955456004439398699669751249623406199542605271188909145969364476344963078599240058180033000440459281558347909876143313940657252737586803051935392596519226965519859474501391969755712097119163926672753588797180811711004203301
q = 105909195259921349656664570904199242969110902804477734660927330311460997899731622163728968380757294196277263615386525795293086103142131020215128282050307177125962302515483190468569376643751587606016315185736245896434947691528567696271911398179288329609207435393579332931583829355558784305002360873458907029141
d = invert(e,(p-1)*(q-1))
m = pow(c,d,n)
print(long_to_bytes(m))

BJD{Advanced_mathematics_is_too_hard!!!}

Buuoj rsa2

  1. 题目是一个py文件，具体如下： 
1
2
3
4
5
N = 101991809777553253470276751399264740131157682329252673501792154507006158434432009141995367241962525705950046253400188884658262496534706438791515071885860897552736656899566915731297225817250639873643376310103992170646906557242832893914902053581087502512787303322747780420210884852166586717636559058152544979471
e = 46731919563265721307105180410302518676676135509737992912625092976849075262192092549323082367518264378630543338219025744820916471913696072050291990620486581719410354385121760761374229374847695148230596005409978383369740305816082770283909611956355972181848077519920922059268376958811713365106925235218265173085

import hashlib
flag = "flag{" + hashlib.md5(hex(d)).hexdigest() + "}"

  1. 通过RSA Wiener Attack（维纳攻击）求得
    d=8920758995414587152829426558580025657357328745839747693739591820283538307445

  2. 当在Python3环境下求解flag时报错，提示要先编码。但是我尝试用utf-8和latin1编码再求md5后，得到的flag提交还是不对，有点坑，最后还是用的Python2，flag的那行代码不需要修改。最终结果为：
    flag{47bf28da384590448e0b0d23909a25a4}

[BJDCTF2020]RSA

题目代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
from Crypto.Util.number import getPrime,bytes_to_long

flag=open("flag","rb").read()

p=getPrime(1024)
q=getPrime(1024)
assert(e<100000)
n=p*q
m=bytes_to_long(flag)
c=pow(m,e,n)
print c,n
print pow(294,e,n)

p=getPrime(1024)
n=p*q
m=bytes_to_long("BJD"*32)
c=pow(m,e,n)
print c,n

'''
output:
12641635617803746150332232646354596292707861480200207537199141183624438303757120570096741248020236666965755798009656547738616399025300123043766255518596149348930444599820675230046423373053051631932557230849083426859490183732303751744004874183062594856870318614289991675980063548316499486908923209627563871554875612702079100567018698992935818206109087568166097392314105717555482926141030505639571708876213167112187962584484065321545727594135175369233925922507794999607323536976824183162923385005669930403448853465141405846835919842908469787547341752365471892495204307644586161393228776042015534147913888338316244169120  13508774104460209743306714034546704137247627344981133461801953479736017021401725818808462898375994767375627749494839671944543822403059978073813122441407612530658168942987820256786583006947001711749230193542370570950705530167921702835627122401475251039000775017381633900222474727396823708695063136246115652622259769634591309421761269548260984426148824641285010730983215377509255011298737827621611158032976420011662547854515610597955628898073569684158225678333474543920326532893446849808112837476684390030976472053905069855522297850688026960701186543428139843783907624317274796926248829543413464754127208843070331063037
381631268825806469518166370387352035475775677163615730759454343913563615970881967332407709901235637718936184198930226303761876517101208677107311006065728014220477966000620964056616058676999878976943319063836649085085377577273214792371548775204594097887078898598463892440141577974544939268247818937936607013100808169758675042264568547764031628431414727922168580998494695800403043312406643527637667466318473669542326169218665366423043579003388486634167642663495896607282155808331902351188500197960905672207046579647052764579411814305689137519860880916467272056778641442758940135016400808740387144508156358067955215018
979153370552535153498477459720877329811204688208387543826122582132404214848454954722487086658061408795223805022202997613522014736983452121073860054851302343517756732701026667062765906277626879215457936330799698812755973057557620930172778859116538571207100424990838508255127616637334499680058645411786925302368790414768248611809358160197554369255458675450109457987698749584630551177577492043403656419968285163536823819817573531356497236154342689914525321673807925458651854768512396355389740863270148775362744448115581639629326362342160548500035000156097215446881251055505465713854173913142040976382500435185442521721  12806210903061368369054309575159360374022344774547459345216907128193957592938071815865954073287532545947370671838372144806539753829484356064919357285623305209600680570975224639214396805124350862772159272362778768036844634760917612708721787320159318432456050806227784435091161119982613987303255995543165395426658059462110056431392517548717447898084915167661172362984251201688639469652283452307712821398857016487590794996544468826705600332208535201443322267298747117528882985955375246424812616478327182399461709978893464093245135530135430007842223389360212803439850867615121148050034887767584693608776323252233254261047
'''

分析

  1. 前半部分可以得到（c,n,x已知）：
      $c=m^{e}\ mod\ n$
    对第二个print出来的值如果设为x，有：
      $x=294^{e}\ mod\ n$

  2. 后半部分有（c2,m2,n2已知）：
      $c2=m2^{e}\ mod\ n2$

  3. 解题首要目标自然是e，由于1中第二个表达式数值较小，本打算用sage求离散对数得到e但是跑不出来，所以用Python进行0，100000的遍历找这个e的值 

1
2
3
4
5
n = 13508774104460209743306714034546704137247627344981133461801953479736017021401725818808462898375994767375627749494839671944543822403059978073813122441407612530658168942987820256786583006947001711749230193542370570950705530167921702835627122401475251039000775017381633900222474727396823708695063136246115652622259769634591309421761269548260984426148824641285010730983215377509255011298737827621611158032976420011662547854515610597955628898073569684158225678333474543920326532893446849808112837476684390030976472053905069855522297850688026960701186543428139843783907624317274796926248829543413464754127208843070331063037
x = 381631268825806469518166370387352035475775677163615730759454343913563615970881967332407709901235637718936184198930226303761876517101208677107311006065728014220477966000620964056616058676999878976943319063836649085085377577273214792371548775204594097887078898598463892440141577974544939268247818937936607013100808169758675042264568547764031628431414727922168580998494695800403043312406643527637667466318473669542326169218665366423043579003388486634167642663495896607282155808331902351188500197960905672207046579647052764579411814305689137519860880916467272056778641442758940135016400808740387144508156358067955215018
for e in range(0,100000):
    if pow(294,e,n) == x:
        print(e)

得到e=52361

  1. 然后希望求得p,q的值以求d。但是想直接分解n的值太困难了。这里n和n2已知，且它们有最大公因数q，可直接求得，所以解题代码如下： 
1
2
3
4
5
6
7
8
9
10
11
12
from Crypto.Util.number import *
from gmpy2 import *

c = 12641635617803746150332232646354596292707861480200207537199141183624438303757120570096741248020236666965755798009656547738616399025300123043766255518596149348930444599820675230046423373053051631932557230849083426859490183732303751744004874183062594856870318614289991675980063548316499486908923209627563871554875612702079100567018698992935818206109087568166097392314105717555482926141030505639571708876213167112187962584484065321545727594135175369233925922507794999607323536976824183162923385005669930403448853465141405846835919842908469787547341752365471892495204307644586161393228776042015534147913888338316244169120
n = 13508774104460209743306714034546704137247627344981133461801953479736017021401725818808462898375994767375627749494839671944543822403059978073813122441407612530658168942987820256786583006947001711749230193542370570950705530167921702835627122401475251039000775017381633900222474727396823708695063136246115652622259769634591309421761269548260984426148824641285010730983215377509255011298737827621611158032976420011662547854515610597955628898073569684158225678333474543920326532893446849808112837476684390030976472053905069855522297850688026960701186543428139843783907624317274796926248829543413464754127208843070331063037
n2 = 12806210903061368369054309575159360374022344774547459345216907128193957592938071815865954073287532545947370671838372144806539753829484356064919357285623305209600680570975224639214396805124350862772159272362778768036844634760917612708721787320159318432456050806227784435091161119982613987303255995543165395426658059462110056431392517548717447898084915167661172362984251201688639469652283452307712821398857016487590794996544468826705600332208535201443322267298747117528882985955375246424812616478327182399461709978893464093245135530135430007842223389360212803439850867615121148050034887767584693608776323252233254261047
e = 52361
q = gcd(n,n2)
p = n // q
d = invert(e,(p-1)*(q-1))
flag = pow(c,d,n)
print(long_to_bytes(flag))

BJD{p_is_common_divisor}

[NCTF2019]babyRSA

题目代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
from Crypto.Util.number import *
from flag import flag

def nextPrime(n):
    n += 2 if n & 1 else 1
    while not isPrime(n):
        n += 2
    return n

p = getPrime(1024)
q = nextPrime(p)
n = p * q
e = 0x10001
d = inverse(e, (p-1) * (q-1))
c = pow(bytes_to_long(flag.encode()), e, n)

# d = 19275778946037899718035455438175509175723911466127462154506916564101519923603308900331427601983476886255849200332374081996442976307058597390881168155862238533018621944733299208108185814179466844504468163200369996564265921022888670062554504758512453217434777820468049494313818291727050400752551716550403647148197148884408264686846693842118387217753516963449753809860354047619256787869400297858568139700396567519469825398575103885487624463424429913017729585620877168171603444111464692841379661112075123399343270610272287865200880398193573260848268633461983435015031227070217852728240847398084414687146397303110709214913
# c = 5382723168073828110696168558294206681757991149022777821127563301413483223874527233300721180839298617076705685041174247415826157096583055069337393987892262764211225227035880754417457056723909135525244957935906902665679777101130111392780237502928656225705262431431953003520093932924375902111280077255205118217436744112064069429678632923259898627997145803892753989255615273140300021040654505901442787810653626524305706316663169341797205752938755590056568986738227803487467274114398257187962140796551136220532809687606867385639367743705527511680719955380746377631156468689844150878381460560990755652899449340045313521804

解题过程

参考1
参考2

  1. e,d已知，先确定$ed-1$的位数。 
1
2
3
4
5
6
7
8
import gmpy2

d = 19275778946037899718035455438175509175723911466127462154506916564101519923603308900331427601983476886255849200332374081996442976307058597390881168155862238533018621944733299208108185814179466844504468163200369996564265921022888670062554504758512453217434777820468049494313818291727050400752551716550403647148197148884408264686846693842118387217753516963449753809860354047619256787869400297858568139700396567519469825398575103885487624463424429913017729585620877168171603444111464692841379661112075123399343270610272287865200880398193573260848268633461983435015031227070217852728240847398084414687146397303110709214913
c = 5382723168073828110696168558294206681757991149022777821127563301413483223874527233300721180839298617076705685041174247415826157096583055069337393987892262764211225227035880754417457056723909135525244957935906902665679777101130111392780237502928656225705262431431953003520093932924375902111280077255205118217436744112064069429678632923259898627997145803892753989255615273140300021040654505901442787810653626524305706316663169341797205752938755590056568986738227803487467274114398257187962140796551136220532809687606867385639367743705527511680719955380746377631156468689844150878381460560990755652899449340045313521804
e = 0x10001

x = gmpy2.log2(e*d-1)
print(x)

结果为：2063.2545176257354

  1. p的位数为1024，q在p的附近所以大致也是1024位。$\phi(n)$的位数约为2048，而$ed-1$大概是2063~2064位，所以$ed-1=1+x\phi(n)$中的x的位数为15~16。
  2. 在$2^{15}$~$2^{16}$减遍历x，找到可以被x整除的$ed-1$。那么有$\phi(n)=\frac{ed-1}{x}$
  3. 找到这个$\phi(n)$，因此p和q大小相近，可以取$\phi(n)$平方根，在其附近的素数取为p，得到p值就很容易找到q，只要它们都是素数，将它们相乘得到n，随即得到明文。
  4. 解题代码： 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
from Crypto.Util.number import *
from gmpy2 import *
from sympy import *

d = 19275778946037899718035455438175509175723911466127462154506916564101519923603308900331427601983476886255849200332374081996442976307058597390881168155862238533018621944733299208108185814179466844504468163200369996564265921022888670062554504758512453217434777820468049494313818291727050400752551716550403647148197148884408264686846693842118387217753516963449753809860354047619256787869400297858568139700396567519469825398575103885487624463424429913017729585620877168171603444111464692841379661112075123399343270610272287865200880398193573260848268633461983435015031227070217852728240847398084414687146397303110709214913
c = 5382723168073828110696168558294206681757991149022777821127563301413483223874527233300721180839298617076705685041174247415826157096583055069337393987892262764211225227035880754417457056723909135525244957935906902665679777101130111392780237502928656225705262431431953003520093932924375902111280077255205118217436744112064069429678632923259898627997145803892753989255615273140300021040654505901442787810653626524305706316663169341797205752938755590056568986738227803487467274114398257187962140796551136220532809687606867385639367743705527511680719955380746377631156468689844150878381460560990755652899449340045313521804
e = 0x10001
p = 0
q = 0
for x in range(2**15,2**16):
    if (e*d - 1) % x == 0:
        phn = (e*d - 1) // x
        p = nextprime(iroot(phn,2)[0])
        q = phn // (p-1) + 1
        if isPrime(q) and isPrime(p):
            print(p, q)
            break
# p = 143193611591752210918770476402384783351740028841763223236102885221839966637073188462808195974548579833368313904083095786906479416347681923731100260359652426441593107755892485944809419189348311956308456459523437459969713060653432909873986596042482699670451716296743727525586437248462432327423361080811225076497
# q = 143193611591752210918770476402384783351740028841763223236102885221839966637073188462808195974548579833368313904083095786906479416347681923731100260359652426441593107755892485944809419189348311956308456459523437459969713060653432909873986596042482699670451716296743727525586437248462432327423361080811225075839
n = p*q
m = pow(c,d,n)
print(long_to_bytes(m))

NCTF{70u2_nn47h_14_v3ry_gOO0000000d}

Reference

[1] https://baike.baidu.com/item/%E6%89%A9%E5%B1%95%E6%AC%A7%E5%87%A0%E9%87%8C%E5%BE%97%E7%AE%97%E6%B3%95/2029414?fr=aladdin
[2] FlappyPig.CTF特训营
[3] https://www.freebuf.com/articles/database/170814.html?replytocom=249214



----------- 本文结束 -----------




0%