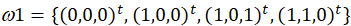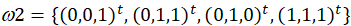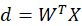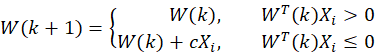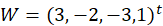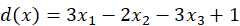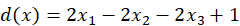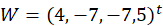感知器算法作业

问题描述

编写感知器算法，求下列模式的解向量：

设

算法介绍

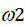
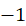
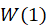
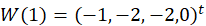
（1）将训练样本写成增广向量的形式，然后规范化（将属于的训练集样本乘以），任取初始权向量开始迭代（这里已经给定为），括号里的1代表迭代次数k=1

（2）用所有的训练样本进行迭代，每输入一个样本X都计算一次

这里的c为校正增量系数，大于0即可。

（3）只要某一轮中有一个样本的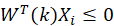则回到（2），直到所有样本训练都正确分类。

计算过程

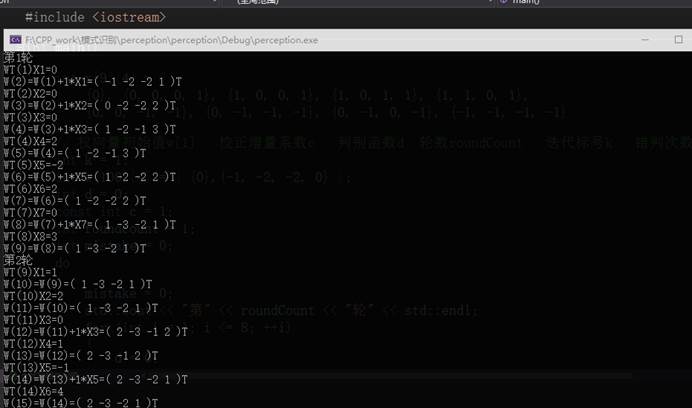
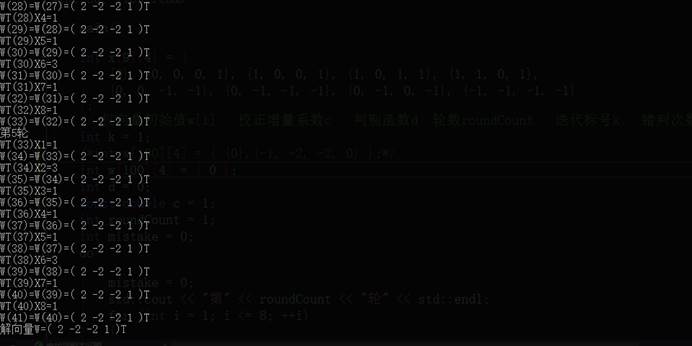
在编写代码时，将计算过程中每一步状态的值都cout出来，当设定初始权向量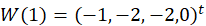，校正增量系数c为1时，有具体过程如下：

由此可得：解向量为

判别函数为

结果分析讨论

（1）当我设定初始权向量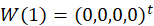，校正增量系数c为1时，有最终的解向量输出结果如下：

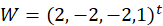
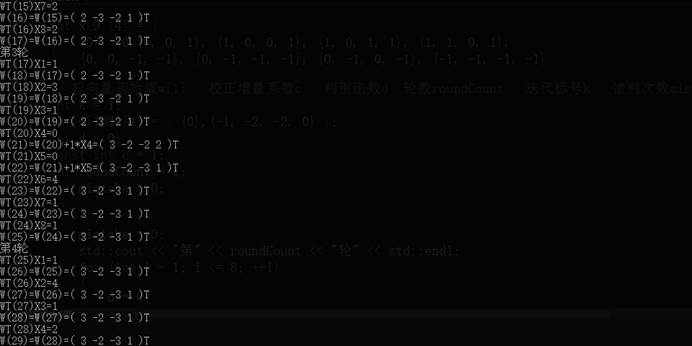
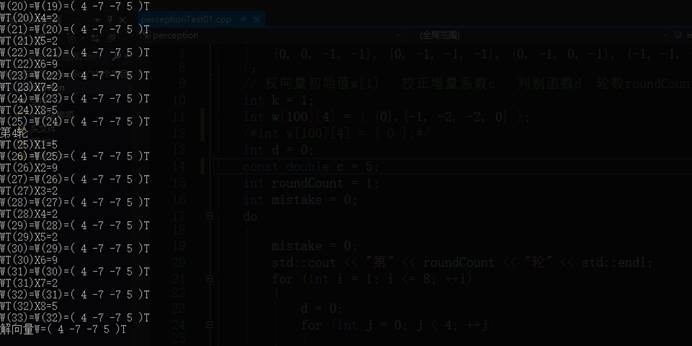
经5轮迭代，此时的解向量为，判别函数为

（2）当设定初始权向量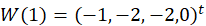，校正增量系数c为4时，有输出结果如下：

迭代4轮后，输出解向量为

由此可得，当初始权向量和校正增量系数取不同值时，输出的结果并不相同，所以感知器算法的解，不是单值的。

附录

#include <iostream>

int main()
{
	int x[9][4] = {
		{0}, {0, 0, 0, 1}, {1, 0, 0, 1}, {1, 0, 1, 1}, {1, 1, 0, 1},
		{0, 0, -1, -1}, {0, -1, -1, -1}, {0, -1, 0, -1}, {-1, -1, -1, -1}
	};
	// 权向量初始值w[1]   校正增量系数c   判别函数d  轮数roundCount   迭代标号k   错判次数mistake
	int k = 1;
	int w[100][4] = { {0},{-1, -2, -2, 0} };
	/*int w[100][4] = { 0 };*/
	int d = 0;
	const double c = 5;
	int roundCount = 1;
	int mistake = 0;
	do
	{
		mistake = 0;
		std::cout << "第" << roundCount << "轮" << std::endl;
		for (int i = 1; i <= 8; ++i)
		{
			d = 0;
			for (int j = 0; j < 4; ++j)
			{
				d += w[k][j] * x[i][j];
			}
			std::cout << "WT(" << k << ")" << "X" << i << "=" << d << std::endl;
			if (d <= 0)
			{
				std::cout << "W(" << k + 1 << ")=" << "W(" << k << ")" << "+" << c
					<< "*X" << i << "=( ";
				for (int j = 0; j < 4; ++j)
				{
					w[k + 1][j] = w[k][j] + c * x[i][j];
					std::cout << w[k + 1][j] << " ";
				}
				std::cout << ")T" << std::endl;
				++mistake;
			}
			else
			{
				std::cout << "W(" << k + 1 << ")=" << "W(" << k << ")=( ";
				for (int j = 0; j < 4; ++j)
				{
					w[k + 1][j] = w[k][j];
					std::cout << w[k + 1][j] << " ";
				}
				std::cout << ")T" << std::endl;
			}
			++k;
		}
		++roundCount;
	} while (mistake > 0);
	std::cout << "解向量W=( ";
	for (int j = 0; j < 4; ++j)
	{
		std::cout << w[k][j] << " ";
	}
	std::cout << ")T" << std::endl;
	std::cin.get();
	return 0;
}